Centripetal Force and Curving Motion
Created by Chinmay Kulkarni
Main Idea

A centripetal force is a force acting on a body while it has curving motion. In these certain situations, the momentum of the system is not constant, since the direction of motion, or velocity always changes direction while the speed may remain constant. For example, image you are kicking a ball that is moving perpendicular to the direction of motion. Now if you keep kicking the ball in this similar manner for a small duration of time, the ball would move in a circular path.
When an object is moving in vertical centripetal motion, for example when a man is swinging on a rope, the force gravity [math]\displaystyle{ mg }[/math] must be accounted with as well as the tension force [math]\displaystyle{ F_t }[/math].
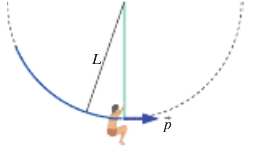
Mathematical Model
While an object is in circular motion, the centripetal force is always perpendicular to the velocity and momentum of the object, meaning that the object experiences a force towards the centre of the circle while it is moving. The simple mathematical model for centripetal force is normally [math]\displaystyle{ F_c = ma_c = \frac{m v^2}{r} }[/math] for any object moving in a circle. However, since this is circular motion, many times the angular velocity ω in radians/second of the system moving is given.
In this case
- [math]\displaystyle{ v = \omega r }[/math]
meaning
- [math]\displaystyle{ F_c = {m\omega^2 r} }[/math]
However sometimes the period of rotation [math]\displaystyle{ T }[/math], in seconds is given
- [math]\displaystyle{ T = \frac{2\pi}{\omega} \,. }[/math]
Thus, the equation becomes
- [math]\displaystyle{ F = m r \left(\frac{2\pi}{T}\right)^2 }[/math]
However in many circumstances, it is helpful to split the centripetal force into parallel and perpendicular forces, or [math]\displaystyle{ F_{para} }[/math] and [math]\displaystyle{ F_{perp} }[/math] respectively.
This means
- [math]\displaystyle{ F_c = F_{para} + F_{perp} }[/math]
Thus we can rewrite the momentum principle as follows
- [math]\displaystyle{ Δp = (F_{para} + F_{perp})Δt }[/math]
Normally, [math]\displaystyle{ F_{para} }[/math] dictates the velocity of the object, while [math]\displaystyle{ F_{perp} }[/math] dictates the direction of motion.
Computational Model
A computational representation of centripetal force can be created using VPython.
We can find the momentum initial position, momentum, and forces in Python.
while t <30000000: rate(100) scene.center=moon.pos/2 scene.range=Earth.radius*60 p_init=mag(pcraft) pcraft_i=pcraft+vector(0,0,0) #craft initial momentum r=Earth.pos-craft.pos #craft initial position from Earth rM=moon.pos-craft.pos #craft initial position from Mon Fgrav=G*mEarth*mcraft/(mag(craft.pos-Earth.pos)**2) #gravity from earth FgravM=G*mcraft*mmoon/(mag(craft.pos-moon.pos)**2) #gravity from moon pcraft=pcraft+r/mag(r)*Fgrav*deltat+rM/mag(rM)*FgravM*deltat #new momentum of the craft based on Earth and Moon
From this we can calculate the change in momentum and the new positions based on the forces.
deltap=pcraft-pcraft_i #calculates change in momentum Fnet=deltap/deltat #calculates Fnet from Earth and Moon p_final=mag(pcraft) Fnet_tangent=((p_final-p_init)/deltat)*norm(pcraft) #calculates Fnet par. Fnet_tangent_arrow.pos=craft.pos Fnet_tangent_arrow.axis=Fnet_tangent*1000000 Fnet_perp=Fnet-Fnet_tangent #calculates Fnet perp Fnet_perp_arrow.pos=craft.pos Fnet_perp_arrow.axis=Fnet_perp*1000000 vcraft=pcraft/mcraft #calculates new velocity of the craft
Examples
Simple
An engineer whose mass is 75 kg holds onto the outer rim of a rotating space station whose radius is 16 m and which takes 45 s to make one complete rotation.
What is the magnitude of the force the engineer has to exert in order to hold on?
- [math]\displaystyle{ F = m r \left(\frac{2\pi}{T}\right)^2 = 75* 16 \left(\frac{2\pi}{45}\right)^2 = 23.39 }[/math]
Middling
Tarzan whose mass is 90 kg is swinging on a vine. At the bottom most point the 8 m long vine breaks. At that point he is traveling at 12 m/s. What was the tension in the vine at the point it broke?
- [math]\displaystyle{ \frac{mv^2}{r} = F_T - mg }[/math]
- [math]\displaystyle{ \frac{90*12^2}{8} = F_T - 90*9.8 }[/math]
- [math]\displaystyle{ F_T = 2502 N }[/math]
Difficult
Tarzan whose mass is 90 kg is swinging on a vine. When the vine makes an angle of 30 degrees with the vertical the 8 m long vine breaks. At that point he is traveling at 11.1 m/s. What was the tension in the vine at the point it broke?
- [math]\displaystyle{ \frac{mv^2}{r} = F_T - mgcos(180-30) }[/math]
- [math]\displaystyle{ \frac{90*11.1^2}{8} = F_T - 90*9.8cos(150) }[/math]
- [math]\displaystyle{ F_T = 2150 N }[/math]
Connectedness
How is this topic connected to something that you are interested in?
- I really enjoy sitting in rollercoasters. Every time I visit any amusement park, that is my number one object, to ride as many rollercoasters as possible. I always feel strange forces on a rollercoaster. ::For example, I feel a sinking feeling overtime I go through a dip and feel light when the car goes over a loop. These sensations are very strange, and sometimes you can feel them in a car as well. ::However, now I know that these are simply forces felt when the normal force is equal to the gravitational force.
How is it connected to your major? Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page