Work
The Main Idea
Work perhaps is a term that most of the people are commonly exposed to. People often use the term "work" to describe their jobs, the amount of energy they had to input to get something done, or even when they describe their gym and their routine exercise. To physicists however, work has a rather specific definition. In physics, work refers to the "efficiency" of the force. A force is doing "work" when acting upon a matter or a particle if it causes the matter to move or change in displacement.
For some people, the new rather absurd concept of work may be a bit confusing. It is important to take consider of the three so called "ingredients" when determining work. Those ingredients are the force, displacement and a cause. The force must "cause" the change in displacement in order to be doing work.
While work may seem like a simple concept, it is nonetheless extremely essential in physics calculations as it is a core aspect of a fundamental principle, the conservation of energy. This will be further discussed in the "connections" part where the individual source of energy work takes part to take role in the transfer of energy from the surrounding to a system or from the system to the surrounding to contribute to the conservation of energy.
A Mathematical Model
There are a few mathematical formulas to determine or calculate the amount of work done by the force. These formulas could be a bit different from situations to situations.
First of all, the formula for work is different according to the consistency of the force.
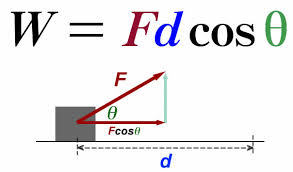
1) When the work is done by a constant force:
[math]\displaystyle{ W=\overrightarrow{F}\bullet\overrightarrow{dr}\cos\theta. }[/math]
It is important to note that when the direction of the force is equal to the direction of the displacement, the "theta" aspect of this equation is equal to 0, meaning that cos(0) will just be 1 and the formula can further be simplified to W = Fd.
2) When the work is done by a non-constant force:
[math]\displaystyle{ W=\int\limits_{i}^{f}\overrightarrow{F}\bullet\overrightarrow{dr} = \sum\overrightarrow{F}\bullet\Delta\overrightarrow{r} }[/math]
This might be a little easier to understand for those who have exposure to calculus. In more of simpler words, the work done by a non-constant force is the product of the summation of the forces that acts upon a system and the change in position of the system. This could be denoted by the usage of a calculus term integral; work is equal to the integral of the force in respect to change in displacement.
3) When work is done by gravity:
[math]\displaystyle{ W = F_g (y_2 - y_1) = F_g\Delta y = - mg\Delta y }[/math]
Notice that this is exact same formula as explained in number one, when the work is done by a constant force, except it is more specified. Theta was neglected because the direction of the gravitational pull was the same as change in height. Notice that this is also similar to the formula for change in potential energy, which is:
[math]\displaystyle{ \Delta PE = mg\Delta y }[/math].
From this we can conclude that:
[math]\displaystyle{ W = -\Delta PE. }[/math]
A Computational Model
The work done on the system by the surrounding is dependent on the system that on decides to choose. For example, if one decides to include earth as a part of the system while calculating the different forms of energies, the work done is 0. However, if one decides to count earth as the surrounding, there is work done by earth but the potential energy from the previous case is eliminated.
Because it is more difficult to use the momentum principle to update position of an object in motion, we typically did not use the earth as a surrounding. Rather, we used earth as part of the system and calculated gravitational force as net force. The example of the code is below;
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
A person picks up a 2kg box from the ground and lifts it up, moves 6 meters forward, and puts the box back down to the ground. What is the work done?
Solution:
The essence of this question is to apply the fact that the direction and the force has to be the same. Did the person apply a force in x direction? No. Thus, the x component of work is 0.
What about the Y component? Yes, the person did work against gravity. The magnitude of the work done when he pulled the box up can be calculated by the product of the mass, the gravitational acceleration, and the change in height (y). However, the overall change in displacement in terms of Y is 0, because he puts it back down.
Thus, the answer for this simple problem is 0.
Middling
Difficult
Connectedness
1. How does this topic contribute to the overall physics?
The concept of work, seemingly an individual concept, is actually an essential part of the fundamental principle, the energy principle. According to the energy principle, the energy of a system is conserved unless the surrounding exerts a force upon the system. This force, when it causes the system to move, is called the work done by surrounding. Thus, it is important to consider work as part of the transitions in energy. Thus, when calculating the final and initial states of the potential and kinetic energy of a system after the work has been done, one can use the following formula:
2. How is this topic connected to something that you are interested in?
I a first year biomedical engineering major so I had to think a bit deeper to answer this question. I have concluded that the concept of work is actually prevalent throughout our body physiology. For example, in order for kinetic energy and potential energy of the muscles cells in our body to be changed, there must be an external force acting upon it changing its displacement. This concept is actually used especially in tissue engineering or biomechanics, which I would love to delve into in the future.
3. Is there an interesting industrial application?
Biomedical engineering is rather distant from the concept of work from other majors. Mechanical Engineering majors have a variety of interesting industrial applications that utilizes the concept of work. For example, when designing the engines of an airplane, mechanical engineers must take account of the work done by the engines of the airplane to win the gravitational pull that would attempt to crash the airplane. Without this concept of work, airplanes would not work.
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Further reading
http://www.physicsclassroom.com/class/energy
External links
https://www.khanacademy.org/science/physics/work-and-energy
Khan academy does a great job in thoroughly explaining the concept of work using visualizations.