Electric Field

CLAIMED BY JAY SHAH PHYS 2212 3/13/2016 EDITED BY YASMIN MARTINS 10/31/2016

This page discusses the general properties of electric fields.

Electric Field

Electric Field is a field created by an electric charge. It is measured in units of newtons per coulomb (N/C), or volts per meter (V/m), and has a direction, making it a vector quantity. The electric field created by a charge exists at all points in space and exerts a force on other charged objects. The field can be drawn as an arrow with tail at the observation location pointing in the direction of the field. The Electric field obeys superposition, so the net Electric field at a point in space can be determined by summing all the individual fields present at that location.

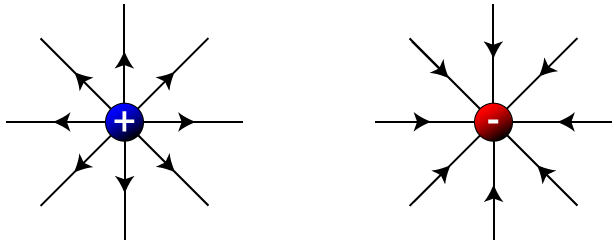
The electric field of a positive particle points away from the particle, while the electric field of a negative particle points toward the particle, as seen right here:

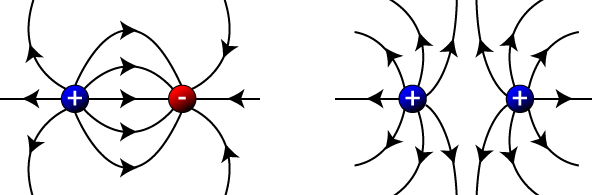
When two oppositely charged particles are placed next to each other, their electric field moves from the positive to the negative. Two similarly charged particles will have fields that are repelled by each other. This is shown below:

Mathematical Concept of a Field

In mathematics, a field is a value that exists at all points in space. The magnitude of an electric field is a scalar. The field itself is represented as a vector: <x,y,z>. Other examples of fields are gravitational fields and magnetic fields.

You can calculate electric field in a few ways. You can calculate the electric field vector and magnitude by using this equation: [math]\displaystyle{ \mathbf{E}=\frac{\mathbf{F}}{q} }[/math].

The magnitude of an electric field can be also be calculated by using the potential difference, Δϕ, between two plates and the distance, d, between them.

[math]\displaystyle{ E = - \frac{\Delta\phi}{d} }[/math]

Electric Field and Force

The force due to an external electric field on a charged particle is given by the equation [math]\displaystyle{ \vec{F} = q\vec{E} }[/math] where q is the charge of the observed particle and E is the electric field. The field created by a charged particle exerts no force on itself. This is to say that the force on a given particle is defined as the charge on that particle multiplied the combined electric fields of the external environment. Since force is measured in Newtons (N) and charge in Coulombs (C), Electric field is measured in Newtons per Coulomb (N/C) as mentioned earlier. Furthermore, the magnitude of an electric field is not dependent on the sign of q (i.e. whether the charge is positive or negative.) The sign only helps determine the direction that the electric field points.

Electric Field and Superposition

The electric field contributed by a charged particle is unaffected by the electric field contributed by other charged particles. To that end, the principle of superposition, as mentioned earlier, states that the net electric field at a location is determined by the sum of all individual electric fields on charged particles. The principle of superposition is very useful to determine the force on a given charged particle. By being able to define electric field as a vector and simply adding up the various components of individual electric fields, the force on a particle is easily calculated using [math]\displaystyle{ \vec{F} = q\vec{E} }[/math]

Electric Field and Electric Potential

Another way to define electric field is using the electric potential over a certain distance to determine field. In this case, Electric field is shown in units volts (V) per meter (m) (V/m).

This page pioneered by --Spennell3 (talk) 13:36, 19 October 2015 (EDT)