Speed and Velocity
by Matt Schoonover
edited by Hyunsu Jo
claimed by Justin Duan (Fall 2016)
claimed by Anthony D'Achille (Spring 2017)
Speed and Velocity
Main Idea
Velocity is a [Vectors vector] quantity, meaning that it has both magnitude and momentum. Speed is the magnitude of a velocity, meaning it's only a scalar without direction. Objects with velocities inherently have a speed and objects with speed don't necessarily have to have a velocity if no direction is specified.
A Mathematical Model
Speed
Speed = [math]\displaystyle{ \sqrt{V_x^2 + V_y^2 + V_z^2} }[/math]
Where [math]\displaystyle{ \boldsymbol{\vec{v}} }[/math] is the velocity vector.
Speed can also be considered as [math]\displaystyle{ \frac{d}{t} }[/math] in a one dimensional sense where you are only concerned about the object's speed in one dimension.
Velocity
Velocity = [math]\displaystyle{ \boldsymbol{\vec{v}} = \frac{\Delta\vec{r}}{\Delta{t}} }[/math]
Where [math]\displaystyle{ {\Delta\vec{r}} }[/math] is the change in the position of the object and t is the time period over which the change in position occurred.
A Computational Model
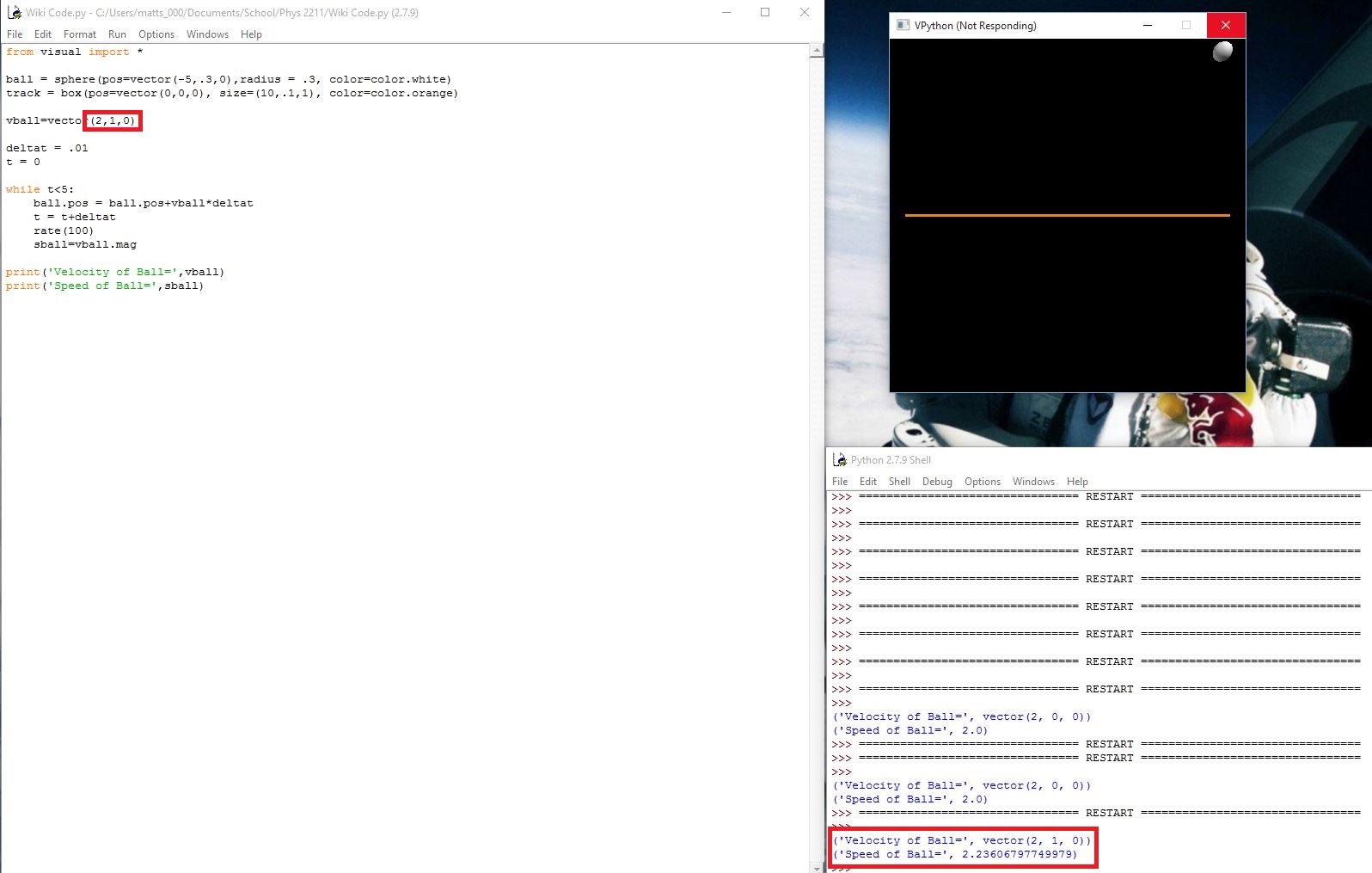
Difference between speed and velocity could be easily explained by the pictures of two computational models.
In the first computational model, the speed which is a scalar quantity(one dimension) is only in x-direction.
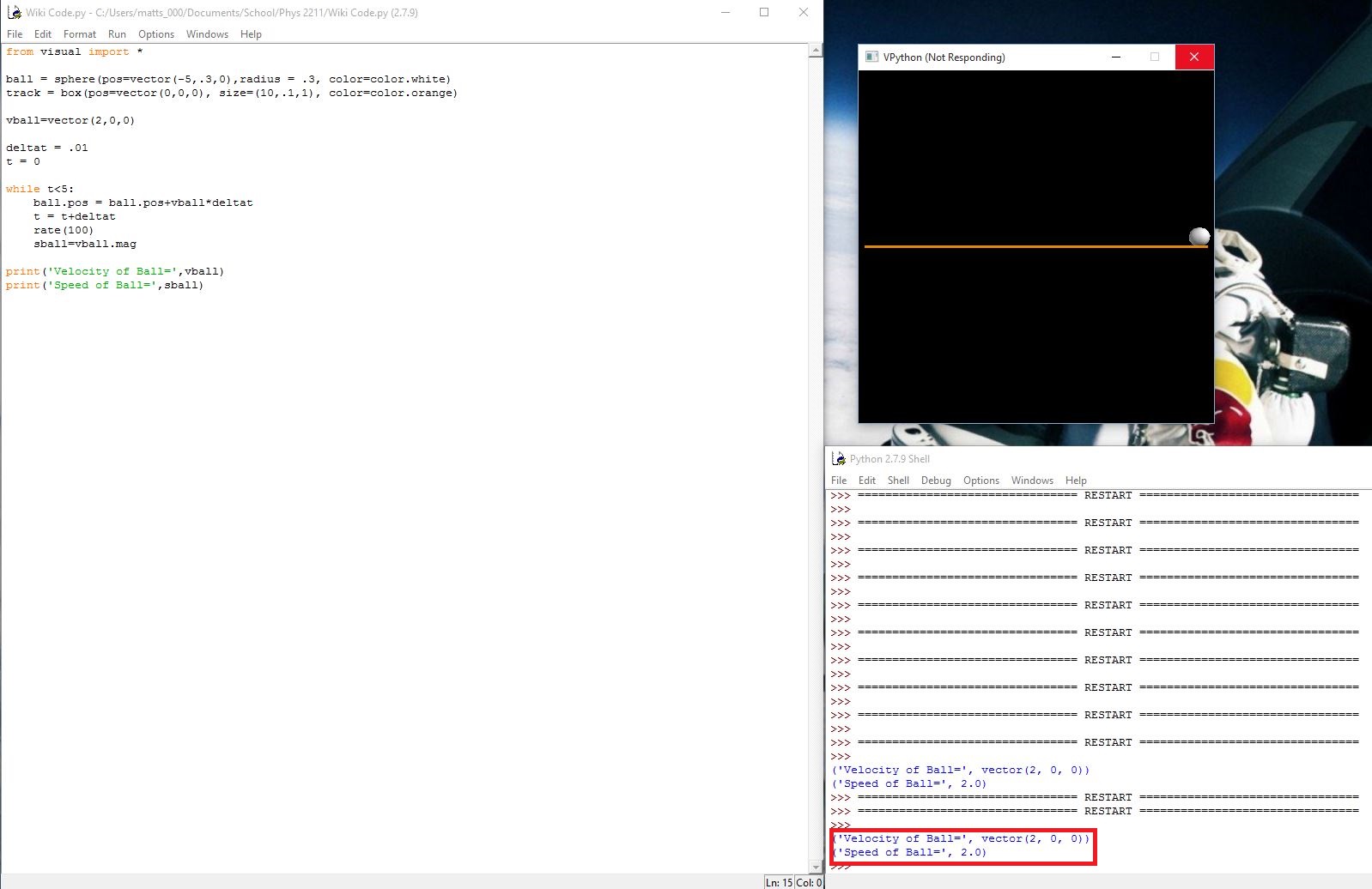
However, in the second computational model, the velocity is in both x and y direction which is in 3 Dimensional <x,y,z> plane which differentiates speed and velocity.
Simple Example
1) What is the average speed of a person who walked a distance of 15 meters in 3 seconds?
This is a problem where we only care about a single dimension, in this case the direction is not specified but is assumed that it's in along the path of the distance.
Using the formula, speed = [math]\displaystyle{ \frac{d}{t} }[/math], where d is 15 meters and t is 3 seconds, the speed is 15/3 = 5 meters per second.
2) Find the velocity of a person who traveled from <0, 0, 10> to <10, 10, 20> in 5 seconds.
Using the formula [math]\displaystyle{ \boldsymbol{\vec{v}} = \frac{\Delta\vec{r}}{\Delta{t}} }[/math], where [math]\displaystyle{ {\Delta\vec{r}} }[/math] is <10, 10, 20> - <0, 0, 10> = <10, 10, 10> and where [math]\displaystyle{ {\Delta{t}} }[/math] is 5,
<10, 10, 10> / 5 = <2, 2, 2>. So the velocity of the person is <2, 2, 2> m/s.
Middling Example
1) At time 0.3 seconds after the tennis ball has been hit by a tennis racket, the tennis ball is located at <4,7,3>m, relative to an origin of the tennis court. At time 0.6 seconds after the tennis ball got hit, it was located at <13, 10, 6>m.
What is the velocity of the tennis ball?
Use the formula: [math]\displaystyle{ \boldsymbol{\vec{v}} = \frac{\Delta\vec{r}}{\Delta{t}} }[/math]
[math]\displaystyle{ {\Delta\vec{r}} }[/math] = <13, 10, 6> - <4, 7, 3> = <9, 3, 3> [math]\displaystyle{ {\Delta{t}} }[/math] = .6 - .3 = .3. <9, 3, 3>/ .3 = <30,10,10> m/s
What is the speed of the tennis ball?
Use the formula: [math]\displaystyle{ \sqrt{V_x^2 + V_y^2 + V_z^2} }[/math]
speed = [math]\displaystyle{ \sqrt{30^2+10^2+10^2} }[/math] = 33.17 m/s
Difficult Example
What is the velocity of an object if the object is traveling in the direction <.566, .793, -.226> at a speed of .04416 km/s?
Knowing the speed is the magnitude of velocity and that velocity is a vector, the original vector can be found by multiplying the magnitude of the vector by the unit vector. Convert km/s to m/s first, .04417 km/s * 1000 m/ 1 km = 44.16 m/s
<.566, .793, -.226> * 44.16 = <24.55, 35.02, -9.98> m/s
Connectedness
Both speed and velocity represents speed of an object. This is why speed and velocity are often interchangeably used in incorrect ways. Speed represents one dimensional speed of an object while velocity represents three dimensional speed of an object with directions of <x,y,z> plane.
The concepts of speed and velocity come up often in different areas of study. In CS there are data structures called graphs that are a bunch of vertices connected by edges, these edges can be similar to speed and velocity in that they can have weights and may or may not have directions.
History
Galileo Galilei, an Italian physicist was the person first credited for measuring speed by taking the distance covered and dividing it by the time. He was famous for his falling bodies experiement and discovered that balls of different masses fell at the same speed. He also attempted to measure the speed of light by having two people hold lanterns and see how long it takes for one person to see the other person's light.
See also
External links
References
Matter and Interactions, Modern Mechanics, 3rd Edition by Chabay and Sherwood.
See also
- Kinds of Matter
- Detecting Interactions
- Fundamental Interactions
- System & Surroundings
- Newton's First Law of Motion
- Newton's Second Law of Motion
- Newton's Third Law of Motion
- Gravitational Force
- Terminal Velocity and Friction Due to Air
- Simple Harmonic Motion
- Electric Polarization
Further Reading
Chapter 1 of Matter and Interactions; Modern Mechanics 4th edition by Chabay and Sherwood
External links
- A physics resource written by experts for an expert audience Physics Portal
- A wiki book on modern physics Modern Physics Wiki
- The MIT open courseware for intro physics MITOCW Wiki
- An online concept map of intro physics HyperPhysics
- Interactive physics simulations PhET
- OpenStax algebra based intro physics textbook College Physics
- The Open Source Physics project is a collection of online physics resources OSP
- A resource guide compiled by the AAPT for educators ComPADRE
References
Matter and Interactions, Modern Mechanics, Volume One 4th Edition by Chabay and Sherwood.