Moment of Inertia for a cylinder
This page discusses the moment of inertia specifically in the case of a cylinder or rod.
Written by Jack Corelli Edited by: Sukanya Basu Spring 2017
A Brief Overview
The Moments of Inertia can be defined as the tendency bodies are resistant to angular motion.
The moment of inertia of an object relates the mass of the object, the distance between the center of mass and the shape of rotation. In a ring, or uniform loop, the center of mass is exactly at the center of the ring, and the moment of inertia can be found by approximating the exterior ring as a single line, akin to a circle. The moment of inertia is dependent on the axis of rotation. In terms of a cylinder, the moment of inertia can be different even if the shape, volume, and mass of the cylinder are the same, given that each cylinder has different axes of revolution.
Governing Equations
Cylinders
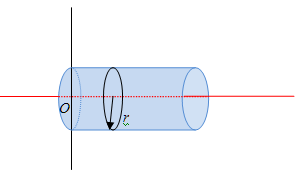
File:Axis3.jpg As seen in the image above, in its simplest form, the moment of inertia can be found for a simple, constant density and shape cylinder by the equation: [math]\displaystyle{ I = \frac{1}{2}*M*R^2 }[/math]
Where I is the moment of inertia, M is the mass of the object being rotated and R is the radius of the rod. This describes the moment of inertia calculated when a rod is spun about its center axis as designated by the red line.
Rods
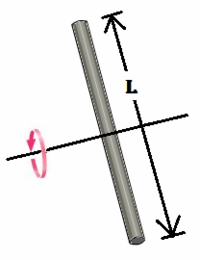
If the axis of rotation is no longer the center of the cylinder or rod, the equations for moment of inertia change distinctly. At the center of a rod, with the axis of rotation perpendicular to the length:
[math]\displaystyle{ I = \frac{1}{4}*M*R^2 + \frac{1}{12}*M*L^2 }[/math]
As can be seen here:
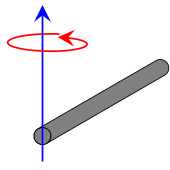
If the axis of rotation has the same direction as the second equation, that is perpendicular to the length, but is at the end of the rod, just touching one of the circular caps, then the equation would be: [math]\displaystyle{ I = \frac{1}{4}*M*R^2 + \frac{1}{3}*M*L^2 }[/math]
As can be seen here:
Examples
Calculate the kinetic energy of a rod rotating about its end given that the rod has mass 200 kg, rotational velocity of 12 m/s, and length 15m, and radius 0.5m:
First, the equation that equals kinetic energy in rotational motion is [math]\displaystyle{ KE = \frac{1}{2}*I*ω^2 }[/math] where [math]\displaystyle{ I = \frac{1}{4}*M*R^2 + \frac{1}{3}*M*L^2 }[/math]
Thus, finding I: [math]\displaystyle{ I = \frac{1}{4}*200*0.5^2 + \frac{1}{3}*200*10^2 }[/math]
[math]\displaystyle{ I = 6679.166 kg*m^2 }[/math]
Thus [math]\displaystyle{ KE = \frac{1}{2}*6679.166 *kg*m^2*(12 \frac{m}{s})^2 }[/math]
[math]\displaystyle{ KE = 480900 J }[/math]
Connectedness
- How is this topic connected to something that you are interested in?
Moments of Inertia are very important in industrial processes, especially for engines. Think of a wind turbine. That is essentially the third equation above, and if an engineer wanted to figure out how much force would be needed to slow the blade, that is one of the components in that equation. But also, due to the torque applied to the blade, there would need to be a slow negative acceleration, so as to not break the wind turbine.
See also
You can find more information in the text book about moments of inertia for different sized objects.
External links
https://en.wikipedia.org/wiki/List_of_moments_of_inertia
http://hyperphysics.phy-astr.gsu.edu/hbase/mi.html
https://www.quora.com/What-is-an-explanation-in-simple-words-of-the-moment-of-inertia
http://www.engineeringtoolbox.com/moment-inertia-torque-d_913.html