Edited by Josh Whitley Spring 2016, Emilie Pourchet Fall 2016

CLAIMED BY WILLIAM NUTE FALL 2017

Potential difference is a scalar quantity; this means it has no direction and only a magnitude. Moreover, potential difference is also a "path independent" quantity. This means that given two different observation locations, the potential difference between those two locations will always be the same no matter what path is taken between them (similar to work, only here we use electric fields rather than forces). The path independent nature of potential helps to simplify electric potential calculations and enables us to solve problems more easily by allowing us to define paths to simplify calculations.

Why is Potential Path Independent?

Before discussing the path independence of electric potential, it can help to review the concept and rationalize why it might be a path independent quantity based on its characteristics.

Electric potential is essentially a value created to physicists to aid in their calculations. In a similar vein to electric field, which is a convenient way to generalize the force exerted on a particle of unit charge place at a given location, potential is a way to generalize the electric potential energy of a particle of unit charge placed at a given location. By nature, electric potential requires 2 points to define it (hence the term "potential difference"), so you will often hear something like "potential difference between A and B". If the potential of a single point is ever mentioned, it's typically in reference to the potential difference between that point and an arbitrary point infinitely far away from all sources of electric field.

So, in essence, electric field, electric potential, and potential difference are the "electric analogues" of force, potential energy, and work. Think for a minute about the relationship between force and work. Work is a path-independent quantity; no matter which way you push an object, how circuitous or direct your route is, the work required to get from one point to another is always the same. Given the analogy, it's not much of a stretch to conclude that potential difference, the electric analogue of work, is similarly a path independent quantity.

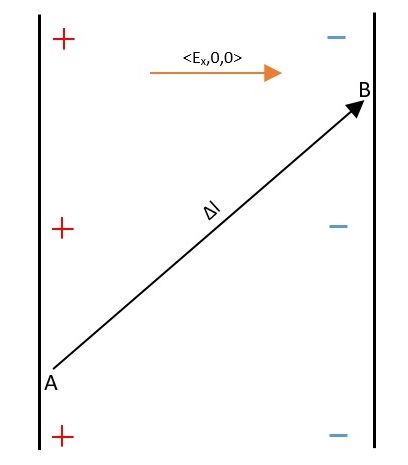
Another way of seeing the path independent nature of V is to look at the equation itself! The definition of potential is formally written as the following [math]\displaystyle{ \Delta V = \vec{E}\bullet \Delta \vec{l} }[/math]

Path Independence

Now that we know some logical reasoning behind why potential has the quality of path independence, what is it?

Path independence is a very useful quality for a value to have. If a value is path independent, then by definition we don't care about any of the information along a path that a particle takes; in other words, we only care about the endpoints of that path. This is a property that allows us to define [math]\displaystyle{ V_{AB} = V_B - V_A }[/math] in the first place.

Moreover, path independence allows us to do some tricks when calculating potential difference. Calculating potential difference for a path through constant electric field is much simpler than calculating potential difference for a path through changing electric field - the latter requires you to integrate an electric field expression, which often times can get messy. By taking advantage of path independence, it's often possible to draw a path from one point to another such than you are always moving along a constant electric field, only having the field change when you are moving perpendicular to it (hence, making potential difference zero).

In more formal notation, you could see something like this: [math]\displaystyle{ V_{AB} = (V_B - V_1) + (V_1 - V_2) + ... + (V_{n-1} - V_n) + (V_n - V_A) }[/math] where 1, 2,..., n are all different points.

Visually, this would look like splitting up a path going straight from A to B into a path that goes from A to n, then to n-1, so on and so forth until point 2, then 1, then finally B.

The general representation of electric potential is the following:

[math]\displaystyle{ \triangle V = V_b-V_a }[/math]

This formula can be expanded by summing the different components of the change in position within electric field components to calculate the change in electric potential. This equation is useful for proving path independence as it can be applied to multi-step path in straight line increments, proving when compared to a direct path that the change in electric potential is the same.

[math]\displaystyle{ \triangle V = -(E_x \triangle x, E_y \triangle y, E_z \triangle z) }[/math]

A Computational Model

[1]

Click the above link to go to a GlowScript page that details Path Independence of Electric Potential. Point A is marked by a green sphere, Point B is marked by a red sphere, moving negative particle 1 is marked by a blue sphere and trail, while moving negative particle 2 is marked by a white sphere and trail. Remember to scroll down in the display window to make sure you've seen the most recent printed value!

In this simulation, you can:

1) Click the display window to progress the simulation, which will print a change in electric potential below corresponding to the parameters of your electric field and the size of your movement. By default, the electric field is (-50,0,0) N/C and the steps are arbitrary and simply designed to show a progression from point A to B by the particle.

2) See how two different paths (one blue and one white) result in the same change in electric potential, regardless of their stark differences in path length.

Note that if you have difficulty seeing the simulation or the printed values, you can navigate to the menu in the top left of the coding window (represented by three parallel bars) and engage a fullscreen mode. Note also that the default code is set to use an electric field with only an x component, for simplicity. Changes in the size of the movement steps are not supported.

Examples

Example 1

Below is an example that demonstrates the path independence of electric potential difference.

Let's calculate the potential difference between A and B in the first scenario. Assume that the height difference between A and B is y and the x component increases by x.

[math]\displaystyle{ \triangle V= -(E_x \triangle x, E_y \triangle y, E_z \triangle z) }[/math]

[math]\displaystyle{ \triangle V= -E_x(x_1-0) + 0(y_1-0) + 0*0 }[/math]

[math]\displaystyle{ \triangle V = -E_xx_1 }[/math]

In the second scenario, let's divide this process into two parts to follow the path outlined from A to C and from C to B.

From A to C:

[math]\displaystyle{ \triangle V = -(E_x \triangle x, E_y \triangle y, E_z \triangle z) }[/math]

[math]\displaystyle{ \triangle V = -E_x(x_1-0)+ 0*0 + 0*0 }[/math]

[math]\displaystyle{ \triangle V = -E_xx_1 }[/math]

From C to B:

[math]\displaystyle{ \triangle V = -(E_x \triangle x, E_y \triangle y, E_z \triangle z) }[/math]

[math]\displaystyle{ \triangle V = -E_x*0 + 0*(y-0) + 0*0 }[/math]

[math]\displaystyle{ \triangle V = 0 }[/math]

Now let's calculate the TOTAL potential difference for this scenario, it is the sum of the potential differences from A to B and from B to C.

[math]\displaystyle{ \triangle V_{A to B} = \triangle V_{A to C} + \triangle V_{C to B} }[/math]

[math]\displaystyle{ \triangle V_{total} = -E_xx_1 + 0 = -E_xx_1 }[/math]

We can see that the results for both scenarios are the same, therefore the electric potential difference is independent of the path taken to calculate it.

Example 2

The above problem deals with a triple-plated, double-spaced, and parallel-plated capacitor and the associated potential difference as you cross over the center plate. Note that, intuitively, the electric fields are only multiplied by the portion of the path that falls within their respective capacitor space. They are then summed. This problem also deals with potential difference when path is reversed.

In order to make this problem demonstrate Path Independence specifically, simply take a new path from A to B (by creating points in between) and calculate the displacement components times the corresponding electric field component of those mid points instead of the direct A to B path. You will find that all Y and Z components equal 0, which leaves only the X component of the path to be calculated. This will inevitably end up with the same potential difference as what is done above.

Connectedness

How is this topic connected to something that you are interested in? How is it connected to your major?

Spontaneous redox reactions often cause a potential disparity that can drive batteries. Electrochemistry, a subset of chemistry that I am interested in as an aspiring chemical engineer, spends a significant amount of time focusing on these interactions and the electrical output of different reaction combinations. In a sense, understanding the physics side of electrical potential helps round out my understanding of electrochemistry.

Is there an interesting industrial application?

In terms of strictly applying the idea of path independence, I would argue there is no industrial application. Though I would argue that related fields, such as electrochemistry, have sweeping industrial applications. The optimization of batteries relies partially on finding half reaction combinations that yield the largest positive potential. It's just that strictly dealing with path independence doesn't leave much room for innovation or invention - you need to involve related ideas. Perhaps the pathing of chemicals inside of a battery is made moot by this principle.

History

Around 1800 an Italian doctor named Luigi Galvani found that touching a frog's leg to two different metals caused it to twitch. Alessandro Volta, a contemporary and rival or Galvani, studied these findings and concluded that a kind of electrical potential difference between the two metals caused a charge to flow through the frog's leg, firing the muscles to ultimately create a post-mortem twitch.

Volta found that, in the presence of significant electrical potential between two metals, electrical charge can flow through a metal wire (and through frog legs, salinated brine, etc). The analogy of the time was that current flowed through wire similarly to water in a pipe. Because of this discovery, Volta lives on through the concept of voltage and the associated unit of measurement - the volt.

References

Matter & Interactions volume II by Ruth W. Chabay and Bruce A. Sherwood.

Chapter 16 Webassign Review

http://scienceline.ucsb.edu/getkey.php?key=4026

Path Independence of Electric Potential

Contents

Why is Potential Path Independent?

Path Independence

A Computational Model

Examples

Example 1

Example 2

Connectedness

History

See also

References

Navigation menu