Perpetual Freefall (Orbit)
Claimed by Thomas Lusk (Fall 2017)
The Main Idea
Perpetual free fall, or orbit, is when the force of gravity is equal to the centripetal force of the object’s motion in space. The centripetal force fluctuates based on changes in the object’s tangential velocity. The force of gravity pulls inward on the object, and the centripetal force pushes the object out. When these perpendicular forces are equal, the object will follow a circular path around the massive body which is the source of gravity. The object is in perpetual free fall because gravity is the only force acting upon it, but the velocity continuously prevents the object from just falling towards the earth. This perpetual free fall causes a feeling of weightlessness for the object. In order to enter the state of orbit, the particular conditions described above must be met. The pictures on the right demonstrate this concept. If the tangential velocity is too high, then the object will reach an escape velocity and will continue to travel outward away from the massive object. If the tangential velocity is too low, then the object will fall towards the massive object. For organizations such as NASA or Boeing that utilize satellites, gravity must be overcome to exit the lower atmospheres and make sure their technologies maintain orbit and do not fall back to Earth. This is achieved via perpendicular propulsion and altitude adjustment in lower atmospheres where air resistance is present, or happens when there is a high enough stable velocity outside the Earth's atmosphere.
There are two types of elliptical orbit: closed and open. An open orbit means the orbiting body is moving with at least the escape velocity of the system. Escape velocity is the minimum speed required by the object such that the tangential velocity overcomes the force of gravity allowing the body to be unbound by an orbit. The most common example of this idea is a comet from outside the solar system slinging around a planet and then leaving. A closed orbit occurs when the particle is not moving with at least the escape velocity. This is the traditional case of orbiting. Closed orbits move in the shape of an ellipse except in the very special case of a circular orbit.
A Mathematical Model
Calculating an objects motion is based around the Newton’s law of universal gravitation and the momentum principle which is described by the equation [math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{object} = \vec{F}_{net} }[/math], where [math]\displaystyle{ \vec{F}_{net} }[/math] is equal to the change in the momentum of the object. Gravity is the only force acting on an object which has begun perpetual freefall outside the atmosphere. The gravitational force equation for an object near the surface of the Earth is [math]\displaystyle{ \vec{F}_{gravity}= \lt 0,{mass}_{object}*{a}_{gravity},0\gt }[/math], where a is acceleration due to gravity: -9.8 m/s. Perpetual freefall, however, follows Newton’s law of universal gravitation which is dependent on the mass of both objects, and their distance apart. [math]\displaystyle{ {F}_{gravity} = G \frac{m_1*m_2}{r^2}\ }[/math] where G is the universal gravitation constant: 6.7e-11, r is the distance between the two objects, and m1 and m2 are the masses of both objects respectively.
Because gravity is the only force acting on the object once it is free from Earth's atmosphere, [math]\displaystyle{ {Force}_{gravity} }[/math] is equal to the objects net force. Once net force is calculated, the momentum principle equation is manipulated so that the object's momentum can be updated as a function of the net force acting on the object. The equation [math]\displaystyle{ {\vec{p}_{object_{final}} } = \vec{p}_{object_{initial}}+ \vec{F}_{net}*{\Delta}{t} }[/math] is used where p is the objects momentum and [math]\displaystyle{ \Delta }[/math]t is the change in time between measurements or data points. Once change in momentum is calculated, the velocity of the object can be found using the assumption that [math]\displaystyle{ \vec{velocity}_{average} = \frac{\vec{p}_{object_{final}}}{{mass}_{object}} }[/math]. This velocity value is then used to update the objects position using [math]\displaystyle{ {\vec{r}_{object_{final}} } = \vec{r}_{object_{initial}}+ \vec{velocity}_{average}*{\Delta}{t} }[/math] where r is the object's position.
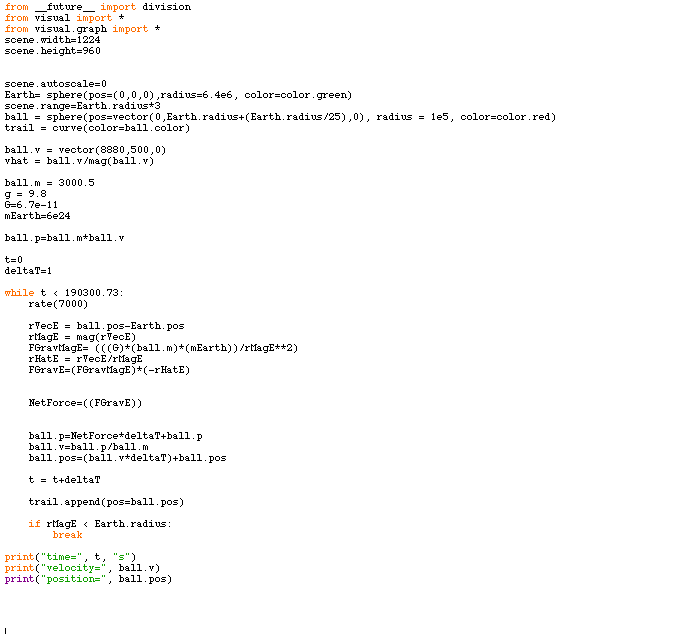
A Computational Model
Below is the computational code written in vPython language. The code consists of a setup of the scene, initial conditions and constants, calculation of force, and an update of momentum, velocity and position. All of these components are expressed visually as a simulation.
Examples
Simple
Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127
Middling
In compliance with MIT OpenCourseWare privacy and terms, the previous example maybe found here [1]
Difficult
In compliance with MIT OpenCourseWare privacy and terms, the previous example maybe found here [2]
Connectedness
Perpetual freefall (orbit) from a frame of reference that it's possible for an object to fall past the curvature of the Earth comparative to an object merely orbiting around the Earth as a constant velocity is an interesting concept that gives a more accurate representation of how objects actually orbit the Earth. The industrial applications of this principle are seen everyday, as companies such as [Boeing], [NASA], and [SpaceX] must use the most basic form of these principles and expand upon it to achieve space and outer atmospheric flight.
Clear understanding of different types of orbits is vital for a number of industries. Many applications of orbitals include spy satellites, communication satellites, space tourism, and space colonization. Without an understanding of orbits everyday things such as satellite TV and cellular communication would not be possible. These ideas may be particularly interesting for students studying aerospace engineering, material science engineering, and mechanical engineering. By understanding off-earth interactions, humans are better equipped to control expansion.
History
The planetary orbits had been observed by astronomers for decades before the first theories on planetary motion were concieved. [| Johannes Kepler] was one of the first to observe and prove that the motions that were being observed were elliptical in nature. From this, [Sir Isaac Newton] was able to combine Kepler's principles with his own theories of motion and that Keplar's theories could be proven by his own theory of gravitation. This derivation led to the relation of a planet's mass to the gravitational force acting on an object which became Newton's gravitational equation used in the calculation of orbits.
Einstein later disproved Newton's methodology as the best model for orbital motion as he explained gravity was due to curvature in space time. As a result of this, astronomers recognized Newtonian physics did not provide the best model of this phenomena. Although Einsteins realistic motion explains orbits the best, Newtonian methods still provide enough accuracy to be used for short term purposes due to their relative simplicity to Einstein's ideas.
See also
[| Law of Gravitation] [| Newton's Laws] [| Momentum Principle] [| Projectile Motion]