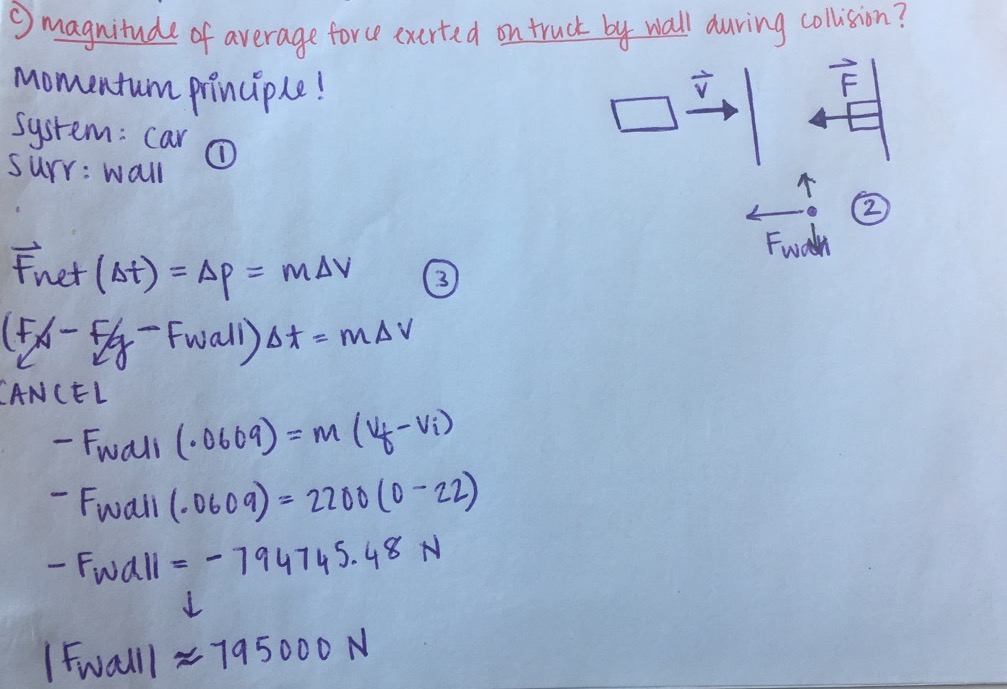Momentum Principle
This page discusses the Momentum Principle and examples of how it is used.
Claimed by Niveda Shanmugam for Spring 2018
Why the Momentum Principle Is Relevant and Everywhere!
The Momentum Principle is a fundamental principle of mechanics and will be used in almost all further problems you will encounter in Physics! The Momentum Principle is applicable to almost all of our everyday activities. While the Momentum Principle is not directly connected to the applications, it is often used in the process (especially in the beginning) of industrial application. For example, when creating life saving airbags and seat belts for cars, the Momentum Principle is used. The final momentum of a car during an accident would be zero, or would stop, and the initial momentum would be based on the mass and velocity of the car. With the change in momentum fixed, the airbag and seat belt would focus on increasing the time taken for the body's momentum to reach zero (final momentum), which would consequently reduce the force of the collision and protect the body from getting as injured.
Another example is in sports! Hitters are often encouraged to "follow-through" when striking a ball, that is, if you follow through with your swing, the bat stays in contact with the ball for a longer period of time. This causes the ball to go farther... Why might this be? It is not because of a greater force, this depends on the impact of the hitter! Instead, this is because an increase in time increases the time of the collision and subsequently contributes to an increase in the velocity change of the ball! By following through, a hitter can hit the ball in such a way that it leaves the bat or racket with more velocity (i.e., the ball is moving faster). In most sports, giving the ball a high velocity often leads to greater success.
The Main Idea
As we know, momentum is given by the product of mass and velocity and is consequently directly proportional to the magnitude of the mass and velocity of any particular object.
The Momentum Principle, also known as the Momentum Conservation Principle, essentially states that for a collision occurring between object 1 and object 2 in an isolated system, the total momentum of the two objects before the collision is equal to the total momentum of the two objects after the collision. This makes sense as it restates Newton's first law ( An object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force). The key word here is "isolated" - when an external force affects the system, momentum can be changed. Overall, the momentum principle assumes that the final momentum is dependent on the initial momentum, the force applied, and the duration in which the force is applied.
A Mathematical Model
The Momentum Principle is defined as [math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{system}= \vec{F}_{net} }[/math] (or [math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math]). As a result, the momentum principle can alternatively be written as [math]\displaystyle{ \vec{p}_{f}=\vec{p}_{i}+\vec{F}_{net}* {∆t} }[/math].
[math]\displaystyle{ \vec{p} }[/math] is the momentum of the system. In the equation, impulse (measured in [math]\displaystyle{ kg*{\frac{m}{s}} }[/math] ) is expressed as the "change in momentum" ([math]\displaystyle{ ∆\vec{p} = \vec{p}_{final} - \vec{p}_{initial} }[/math]), which includes both the magnitude and direction of the momentum. Therefore, momentum is a vector quantity.
[math]\displaystyle{ \vec{F}_{net} }[/math] is the net force from the surroundings. Force (measured in Newtons, or N) includes the interactions between the system and the surroundings, like the gravitational force exerted by the Earth on us or the force that a compressed spring exerts on a mass. Because momentum is defined as a vector, in the Momentum Principle, the force includes both the magnitude and direction. Also, it is important to note that the Momentum Principle calls for the net force, which is the sum of all the different forces from the surroundings. This becomes essential when an object has multiple forces acting on it like the force of gravity, the force of a spring, force of friction, etc. as all of these, keeping in mind their respective directions, have to be added to get the net Force.
To avoid errors, here is a systematic procedure to follow when approaching problems involving this concept:
Step 1: Define system and surroundings.
Step 2: Draw a free body diagram - This is a helpful way to determine the various forces acting on the system.
Step 3: Use the Momentum Principle to calculate the value needed.
Let's follow through an example!
In a crash test, a truck with mass 2200 kg traveling at 22 m/s smashes head-on into a concrete wall without rebounding. The front end crumples so much that the truck is 0.67 m shorter than before.
(a) What is the average speed of the truck during the collision (that is, during the interval between first contact with the wall and coming to a stop)?
Here, we use kinematic equations to solve for average velocity!
(b) About how long does the collision last? (That is, how long is the interval between first contact with the wall and coming to a stop?)
(c) What is the magnitude of the average force exerted by the wall on the truck during the collision?
Notice our 3 step procedure to solve, using the Momentum Principle! We have step 1- our system and surroundings, which helps with step 2- drawing a free body diagram! In our diagram, we can see that the force of the wall points to the left, which helps us then write it as a negative force in our equation (which makes sense, as we see our negative signs then cancel out each other!). We also notice our other forces, depicted by black arrows, but see that they will cancel each other out! Finally, we use our momentum principle in step 3- solving the equation!
A Computational Model
Click on the picture to read a description!
In this example, the ball is not moving, meaning it has a velocity of zero. If the velocity is zero, there is no change in momentum, meaning that net force is also zero. Therefore, we can conclude that initial and final momentum are equal due to the ball not moving. Therefore, [math]\displaystyle{ ∆\vec{p}=0 }[/math], and thus [math]\displaystyle{ \vec{F}_{net} = 0 }[/math]. Because the net force is equal to zero, this means that the force due to tension is equal in magnitude and opposite in direction to the force due to gravity.
[math]\displaystyle{ t }[/math] is the time (measured in seconds, or s). Specifically, the Momentum Principle calls for the "change in time" ([math]\displaystyle{ ∆\vec{t} = \vec{t}_{final} - \vec{t}_{initial} }[/math]), or in other words, the duration of the interaction is needed. Overall, if a force is applied to a system over a greater duration, the change in momentum is greater, as the momentum principle, [math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math], also demonstrates that the change in momentum is directly proportional to the duration of the applied force.
Momentum Principle Continued
The Momentum Principle can be further manipulated to find the change in velocity of the system. This is represented by the formula: [math]\displaystyle{ \vec{v}_{f}=\vec{v}_{i}+{\frac{\vec{F}_{net}}{m}}*{∆t} }[/math].
[math]\displaystyle{ \vec{v}_{f} }[/math] is the final velocity of the system, and [math]\displaystyle{ \vec{v}_{i} }[/math] is the initial velocity of the system. The difference between the two can be shortened to [math]\displaystyle{ \vec{{∆v}} }[/math], and represents the change in velocity of the system.
[math]\displaystyle{ \vec{F}_{net} }[/math] is the net force acting on the system.
[math]\displaystyle{ m }[/math] is the mass of the system.
[math]\displaystyle{ {∆t} }[/math] is the change in time of the system in which it is acted on by the force.
This manipulation of the momentum principle is very useful when it comes to updating the position of the system because it gives you the change in velocity over the observed time interval.
Previous Example Continued
Click on the link to see the Momentum Principle through VPython!
Make sure to press "Run" to see the principle in action!
Here, we see the same ball and spring model from before, except we see the spring oscillating! This is because we start with a momentum (velocity greater than 0) and as the spring and ball move, we update net force. From each new net force, we have a new momentum. This new momentum gives us a new velocity, that we can then add to the ball's previous position to update its location.
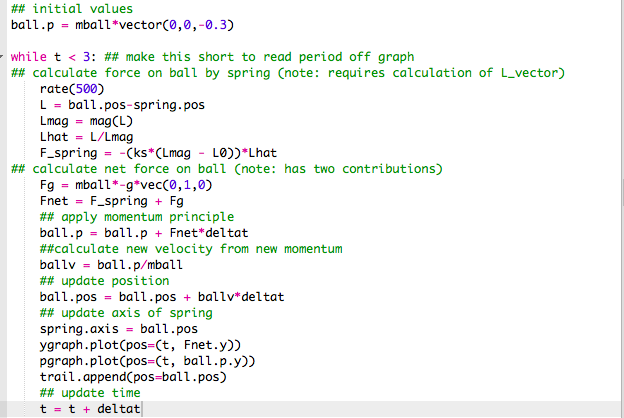
This is depicted in this code:
We will now continue to add arrows depicting gravitational force, spring force, net force, and momentum to gain a better understanding of how each change as the Momentum Principle continues.
Net Force is depicted by the RED arrow. Gravitation Force is depicted by the BLUE arrow, like before. Spring Force is depicted by the WHITE arrow, like before. Momentum arrow is depicted by the ORANGE arrow.
The differences in the code now just allow for arrows to represent each value. You can see these changes here:
Let's Practice!
Simple
Two external forces <60,-70,0>N and <20,10,0>N, act on a system. What is the net force acting on the system?
Answer: <80,-60,0>N
Explanation:
The net force is just synonymous for the overall force acting on the system. In this case, this is the sum of the forces given in the problem above.
[math]\displaystyle{ \vec{F}_{net} = \vec{F}_{1} + \vec{F}_{2} }[/math]
[math]\displaystyle{ \vec{F}_{net} }[/math] = <60,-70,0)N + <20,10,0>N = <80,-60,0>N
Intermediate
A hockey puck is sliding along the ice with nearly constant momentum <16,0,5>kg*m/s when it is suddenly struck by a hockey stick with a force <0,0,2000>N that lasts for only 3 milliseconds (3e-3s). What is the new (vector) momentum of the puck?
Answer: <16,0,11>kg*m/s
Explanation:
In this example, we are manipulating the momentum principle in order to calculate the new momentum at a given time. This is also called the update momentum formula.
[math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math]
[math]\displaystyle{ \vec{p}_{final} - \vec{p}_{initial} }[/math] = [math]\displaystyle{ \vec{F}_{net} * {∆t} }[/math]
[math]\displaystyle{ \vec{p}_{final} }[/math] - <16,0,5>kg*m/s = <0,0,2000>N * (3e-3)s
[math]\displaystyle{ \vec{p}_{final} }[/math] = <16,0,11>kg*m/s
NOTE - Since there is no force in the x and y coordinates, momentum here remains constant.
Difficult
In outer space a rock of mass 5kg is acted on by a constant net force <29,-15,40>N during a 4s time interval. At the end of this time interval the rock has a velocity of <114,94,112>m/s. What is the rock's velocity at the beginning of the time interval?
Answer: <90.8,106,80>m/s
Explanation:
This example is similar to the first example. Only now, instead of manipulating variables to solve for momentum, we must manipulate the variables to solve for velocity, specifically initial velocity. Velocity can be connected to the momentum principle since momentum is just mass multiplied by velocity.
[math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math]
[math]\displaystyle{ \vec{p}_{final} - \vec{p}_{initial} = \vec{F}_{net} * {∆t} }[/math]
[math]\displaystyle{ \vec{p} = m * \vec{v} }[/math]
[math]\displaystyle{ m\vec{v}_{final} - m\vec{v}_{initial} = \vec{F}_{net} * {∆t} }[/math]
(5kg * <114,94,112>m/s) - (5kg * [math]\displaystyle{ \vec{v}_{initial} }[/math]) = <29,-15,40>N * 4s
[math]\displaystyle{ \vec{v}_{initial} }[/math] = <90.8,106,80>m/s
Connectedness
The Momentum Principle is connected to How is it connected to your major? Is there an interesting industrial application? History Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
Further Reading
Read these to get some great further insight on this concept!
[1] http://acme.highpoint.edu/~atitus/phy221/lecture-notes/2-2-momentum-principle.pdf
[2] http://authors.library.caltech.edu/2577/1/TOLpr30c.pdf
As the Momentum Principle is the first of three fundamental principles of mechanics, the next possible topics to examine would be the other fundamental principles, the Energy Principle and the Angular Momentum Principle. Also, although the Momentum Principle is an extremely important concept that usually signals the start of a momentum related problem, the principal branches out into other momentum topics like Impulse and Iterative Prediction, which are used to solve other types of problems.
External links
[2] https://www.youtube.com/watch?v=ZvPrn3aBQG8
References
[1] William Harris "How Newton's Laws of Motion Work" 29 July 2008. HowStuffWorks.com. <https://science.howstuffworks.com/innovation/scientific-experiments/newton-law-of-motion.htm> 11 April, 2018.
[2] Sherwood, Bruce A. "2.1 The Momentum Principle." Matter & Interactions. By Ruth W. Chabay. 4th ed. Vol. 1. N.p.: John Wiley & Sons, 2015. 45-50. Print. Modern Mechanics.
[3] Fenton, Flavio. "Momentum and Second Newton's Law." August-September Lectures. 2017.
[4] “Momentum Conservation Principle.” The Physics Classroom, <www.physicsclassroom.com/class/momentum/Lesson-2/Momentum-Conservation-Principle.>