Projectile Motion

This page will attempt to analyze projectile motion, a branch of classical mechanics in which the motion of an object (the projectile) is analyzed under the influence of the constant acceleration of gravity, after it has been propelled with some initial velocity.

The Main Idea

Projectile motion is a branch of classical mechanics which analyzes the motion of objects (projectiles) under the influence of the constant acceleration of gravity near the surface of the earth. Often, the projectiles are propelled prior to being analyzed under the influence of gravity, giving them initial velocities that affect their trajectories. Two classic examples of projectile motion are the firing of a cannon and throwing a ball off a tower, but there are many other examples of projectile motion. To be considered a projectile the only force which can be acting upon the object is gravity. Traditionally, projectile motion is modeled from instant the propelling force ceases to act on the object to the instant the object hits the ground or is otherwise interrupted.

A Mathematical Model

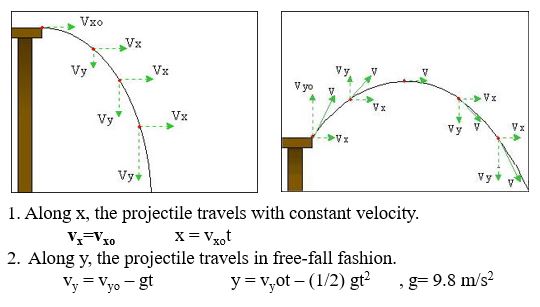
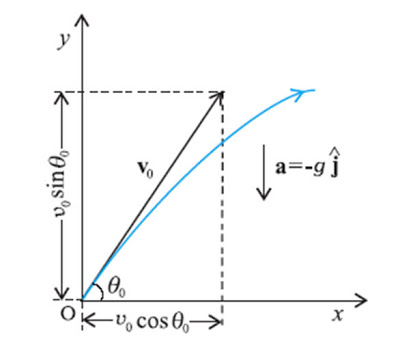
Regardless of the direction of motion of the projectile, the free-body diagram of a projectile is still modeled as an particle on which only one force is acting: gravity. This is the free-body diagram throughout the entire range of motion of the projectile. Note that for real projectiles, other forces such as air resistance are usually present, but these are usually negligible in magnitude and make the mathematical model significantly more complicated, so these are ignored. Traditionally, the Frame of Reference chosen for projectile motion problems places the origin on the ground below the point of launch and considers the time of launch t=0. The +y direction is usually defined as vertically upwards, so the gravitational force acts in the -y direction. The +x direction is usually defined as the direction of the horizontal component of the projectile's velocity. No forces act in the x direction, so the x component of the projectile's velocity is constant throughout the trajectory. The y component of the velocity is constantly changing over time due to the gravitational force. Gravity near the surface of the earth causes a constant downward acceleration of 9.8m/s^2. This causes a parabolic trajectory. The constant velocity in the x direction and the constant acceleration in the y direction lend themselves to the Kinematic Equations. Kinematics are used to analytically solve problems related to projectile motion.

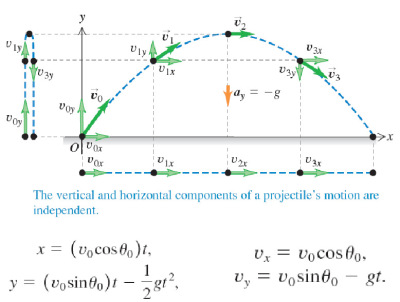
The following equations derived from kinematics describe the x and y components of a projectile's position as functions of time.

[math]\displaystyle{ y(t) = - \frac{1}{2} g * t^2 + v_{y, 0} * t + y_i }[/math]

[math]\displaystyle{ x(t) = v_{x, 0} * t }[/math]

It is evident from the above equations that the two components of a projectile's motion are independent; the particle's horizontal position has no effect on its vertical motion and vice versa.

[math]\displaystyle{ v_{y, 0} }[/math] and [math]\displaystyle{ v_{y, 0} }[/math] may each be positive, negative, or 0, depending on how the projectile was launched, resulting in a variety of trajectory shapes. Below are some possible trajectories of projectiles:

Sometimes, an initial speed and an initial angle (usually with respect to the horizontal) is given. In this case, [math]\displaystyle{ v_{y, 0} = v_0 \sin \Theta_0 }[/math] and [math]\displaystyle{ v_{x, 0} = v_0 \cos \Theta_0 }[/math].

At the highest point in a projectile's trajectory, the projectile's velocity is entirely horizontal; the vertical component is 0. This is because at that point in time, the vertical velocity has stopped being positive and is no longer carrying the projectile higher, but has not yet become negative and has therefore not begun lowering the projectile once more.

A Computational Model

One method used to visualize or predict a projectiles trajectory is to apply our mathematical model using computational programming. Computer models usually use Iterative Prediction rather than Kinematics to determine the path of the projectile. Here is an example of a program in vPython that simulates a projectile:

Simulation of Projectile

Click "view this program" on the top left corner to view the source code.

Examples

A projectile's trajectory, as discovered by Galileo, is modeled with a parabola. The cannon provides a very accurate representation of projectile motion because there is an initial force which has an X component (usually the cannon also has a Y component of force as well, but this is not necessary for projectile motion). This gives the ball the horizontal velocity needed to be a projectile.

You see here that the velocity of the ball can be broken into X and Y components which can then be analyzed separately as the projectile moves along its intended path. The X velocity is constant and the Y velocity accelerates with the force of gravity.

It is important to note that for this analysis we made many simplifying assumptions including, that the acceleration due to gravity remains constant because our object is very close to earth, its size is small enough to be modeled as a point mass where irregularities in shape can be neglected, also there are no resistive forces acting on our object that would affect its motion, such as drag.

Simple Example

In the below example basic of projectile motion, the initial y component of velocity, 0 m/s, and the constant acceleration due to gravity, -9.8 m/s^2 in the y direction can be used to determine the time that the ball is in the air by isolating t in the given example. The constant X component of velocity can be multiplied by the time to give you the final x component of position because it is constant.

Middling Example

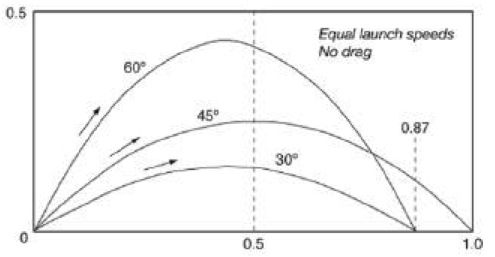
In the example above you can see that the angle from which the cannon launches the affects the distance ball travels. In this example the best angle to launch the ball from in order to get maximum distance traveled is 45 degrees. The easiest way to calculate how far the ball goes is to determine how long it takes for the y component of the velocity to equal zero and then multiply double that time by the x velocity. This works because when the ball's y velocity is 0 the ball has reached the top of the parabola and half of the total motion has occurred.

It is an important observation that the angle of launch affects the distance which the ball travels. The same force applied at the 30, 45, and 60 degree angles yields three different curves of motion. Despite having different curves, each of the three curves are parabolas. 45 degrees always yields the longest distance traveled in the x direction given the same initial force.

Difficult Example

In the example above a staged rocket launches and then ignites its next stage immediately. Once its fuel has been exhausted the rocket follows a free fall trajectory with horizontal motion, or projectile motion. The same basic equations are applied as the previous problems, but you must account for changing angles and multiple forces acting upon the rocket until it becomes true projectile motion.

Connectedness

Understanding projectile motion was necessary for me to construct a Rube Goldberg machine which among other pieces contained a small catapult which launched a ping pong ball into a cup. To make the machine function properly I had to calculate the motion of the ping pong ball to place the cup in a position where it would catch said ball. One interesting industrial application of projectile motion is the creation of scopes for hunting rifles. A scope will usually have crosshair markings indicating the difference in distance of the animal from the hunter with the distance that the scope is calibrated to. This allows the hunter to aim more accurately at the animals he is hunting even if they are at a nonideal location. For example, if a hunter is 210 yards from a deer and his rifle is sighted for 200 yards he can aim at the deer with the dash on the scope which indicates +10 yards, or 10 more yards than his scope is sighted for. To find this distance, the scope makers must calculate the projectile motion of the bullet and determine how much higher to aim the rifle to hit a target 10 more yards away.

History

Major contributions to our current understanding of Projectile Motion

Aristotle

The first findings of Projectile Motion were contributed by Aristotle. He believed that a projectile modeled by a canon ball travels in a straight line until it lost its 'impetus'. When it lost its 'impetus' which ran out after time, due to a restive force, the projectile would immediately drop and fall to the ground. For objects projected over short distances, at first observation this can visually appear to be true.

Galileo

Galileo's findings were motivated by the Renaissance. At the time people were searching for a way to model 3-D objects in our 2-D world. Through as series of experiments he discovered that projectile motion is a result of Free Fall Motion along the y-axis and Uniform Motion along x-axis. This model is more well known and represents a more clearer understanding, one that is more widely accepted modern day.

Galileo proved that the vertical and horizontal motion of an object were unrelated. In other words, two objects will fall to the ground at the same rate if one is launched horizontally from the tower and the other object is simpy dropped. This is because each object has the same initial vertical velocity. Galileo also upended the beliefs of his time by proving that the curve of motion of a projectile was precisely parabolic.

Isaac Newton

Isaac Newton contributed to the idea of Projectile motion with his hypothetical cannon on a mountaintop. This hypothesis is now known as Newton's cannonball. Newton theorized that a cannon on top of a high mountain could fire a ball with varying forces for varying effects. A cannonball dropped off the mountain would merely return to earth, but if that cannonball were fired from a cannon then it would return to Earth in an arc, or parabolic shape. This would be considered projectile motion. Newton also extended this experiment to show universal gravitation, hypothesizing what orbit of the cannonball would look like.