Acceleration
This page defines and describes acceleration.
The Main Idea
Acceleration, denoted by the symbol [math]\displaystyle{ \vec{a} }[/math], is a vector quantity defined as the rate of change of velocity with respect to time.
Acceleration is an instantaneous value, so it may change over time. If this is the case, over any given time interval, there is an average acceleration value denoted [math]\displaystyle{ \vec{a}_{avg}\lt math\gt . The most commonly used metric unit for acceleration is the meter per second per second (m/s/s or m/s\lt sup\gt 2\lt /sup\gt ). ===A Mathematical Model=== Instantaneous acceleration is defined as: \lt math\gt \vec{a} = \frac{d\vec{v}}{d t} }[/math].
Derivative Relationships
Acceleration is the time derivative of velocity, which is in turn the time derivative of position, so acceleration is the second time derivative of position.
Recall that
[math]\displaystyle{ \vec{a}(t) = \frac{d\vec{v}(t)}{dt} }[/math]
and
[math]\displaystyle{ \vec{v}(t) = \frac{d\vec{r}(t)}{dt} }[/math].
Therefore:
[math]\displaystyle{ \vec{a}(t) = \frac{d\vec{v}}{dt} = \frac{d^2\vec{r}}{dt^2} }[/math].
Integral Relationships
The integral of acceleration yields velocity, and the integral of velocity yields position, so the double integral of acceleration yields position.
Recall that:
[math]\displaystyle{ \vec{r}(t) = \int \vec{v}(t) \ dt }[/math]
and
[math]\displaystyle{ \vec{v}(t) = \int \vec{a}(t) \ dt }[/math].
Therefore:
[math]\displaystyle{ \vec{r}(t) = \iint \vec{a}(t) \ dt \ dt }[/math].
Kinematics Equations
The kinematics equations can be derived from the derivative and integral relationships between acceleration, velocity, and displacement.
- [math]\displaystyle{ \vec{v}_{f} = \vec{v}_{i}+{\vec{a}{\Delta t}} }[/math]
- [math]\displaystyle{ \vec{v}^2_{f} = \vec{v}^2_{i}+ 2 {\vec{a}{\Delta x}} }[/math]
- [math]\displaystyle{ \vec{x}_{f} = \vec{x}_{i}+{\vec{v}_{i}{t}}+ 1/2 {\vec{a}}{t}^2 }[/math]
Newton's Second Law of Motion
Force, as a vector quantity, equals mass times acceleration, as a vector.
Another form of acceleration is given by Newton's second law of motion:
- [math]\displaystyle{ \vec{F} = m \vec{a} \quad \to \quad \vec{a} = \vec{F}/m }[/math]
where [math]\displaystyle{ \vec{F} }[/math] is the net force acting on the body, m is the mass of the body, and [math]\displaystyle{ \vec{a} }[/math] is the center-of-mass acceleration.
Why does [math]\displaystyle{ {\vec{F}}= m{\vec{a}} }[/math]?
- This formula can easily be derived from Newton's Second Law: the Momentum Principle.
Recall that:
- [math]\displaystyle{ {\Delta\vec{p}} = {\vec{F}_{net}{\Delta t}} }[/math] and [math]\displaystyle{ {\Delta\vec{p}} = m {\Delta\vec{v}} }[/math]
Therefore:
- [math]\displaystyle{ {\vec{F}} = \frac{\Delta\vec{p}}{\Delta t} = \frac{m {\Delta\vec{v}}}{\Delta t} = m {\frac{\Delta\vec{v}}{\Delta t}} }[/math]
- Note: [math]\displaystyle{ \vec{a} = \frac{\Delta\vec{v}}{\Delta t} }[/math]
Therefore:
- [math]\displaystyle{ {\vec{F}} = \frac{\Delta\vec{p}}{\Delta t} = m\vec{a} }[/math]
A Graphical Model
Here are some examples to help you see acceleration graphically.
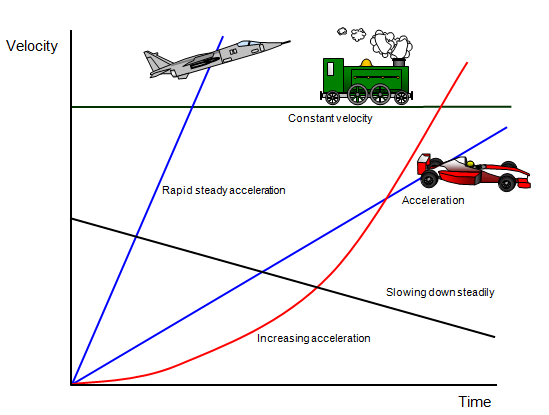
- [Above] Here you can see many different graphs of velocity over time. Notice the difference between an increasing acceleration, constant velocity, and constant acceleration. The slope of the line on a velocity versus time graph is acceleration.
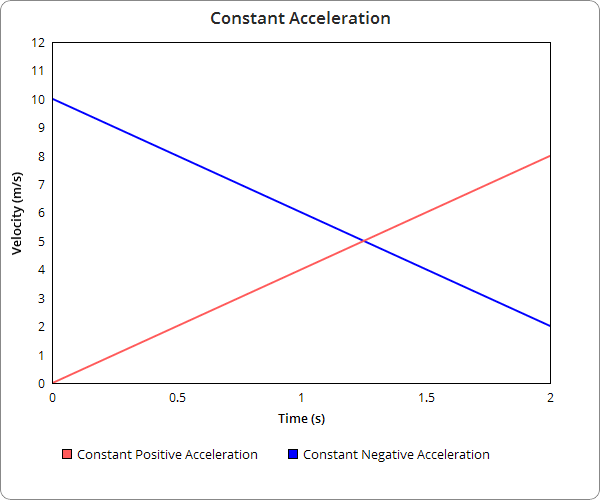
Constant Acceleration
Constant acceleration is shown with straight lines on velocity over time graphs. This means that the velocity is changing by a single constant amount per second. Positive slopes mean that the acceleration is positive, and this means the velocity is constantly increasing. Negative acceleration slopes denote a negative acceleration and decreasing velocity. Lines with zero slope have no acceleration and a constant velocity.
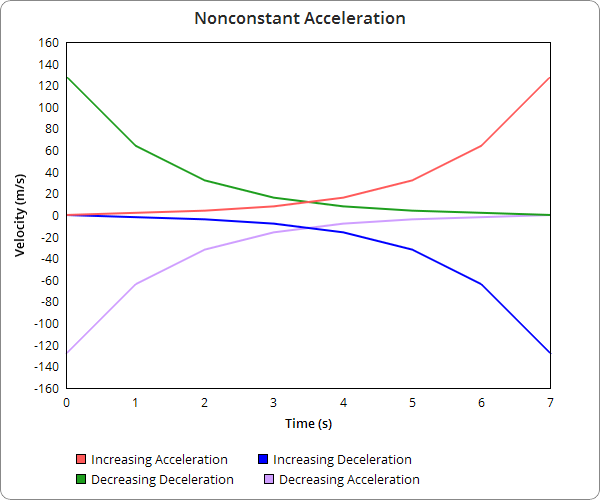
Nonconstant Acceleration
Nonconstant Acceleration is shown with curved lines on velocity over time graphs. Graphs that concave up and are increasing show increasing acceleration, and graphs that concave up and are decreasing show decreasing deceleration. Graphs that concave down and are increasing show decreasing acceleration and graphs that are concave down and decreasing show increasing deceleration.
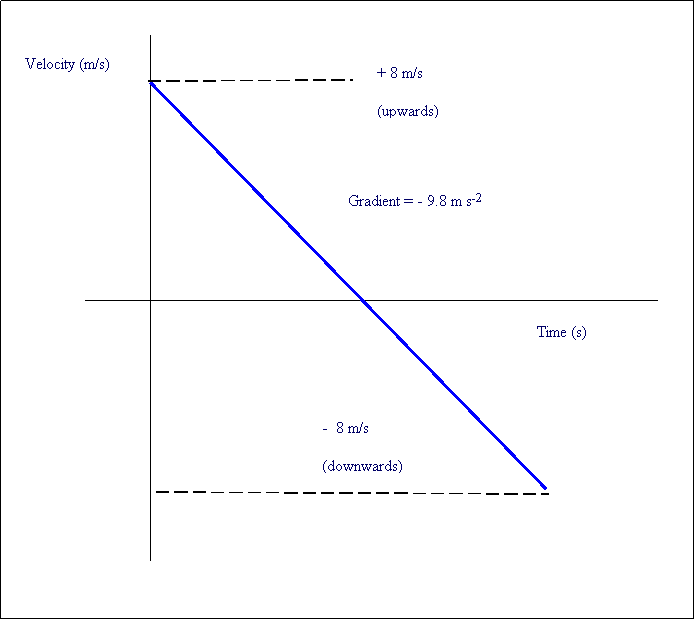
Example
- [Above] Here is a common example showing the velocity of a ball being thrown into the air. Notice that the slope = -9.8 (acceleration due to gravity) and that the graph goes through the x-axis. (The crossover is when the ball is at the highest height and v = 0)
Examples
Here are a couple simple acceleration problems with solutions included:
Question 1

Question:
A motorcycle accelerates uniformly from rest to a speed of 7.10 m/s over a distance of 35.4 m. Determine the acceleration of the motorcycle.
Solution:
Given:
- [math]\displaystyle{ v_i = 0 m/s }[/math]
- [math]\displaystyle{ v_f = 7.10 m/s }[/math]
- [math]\displaystyle{ d = 35.4 m }[/math]
Find:
- [math]\displaystyle{ a = ? }[/math]
Calculations:
- [math]\displaystyle{ v_f^2 = v_i^2 + 2ad }[/math]
- [math]\displaystyle{ 2ad = v_f^2 - v_i^2 }[/math]
- [math]\displaystyle{ a = \frac{v_f^2 - v_i^2}{2*d} }[/math]
- [math]\displaystyle{ a = \frac{(7.10m/s)^2 - (0m/s)^2}{2*35.4m} }[/math]
- [math]\displaystyle{ a = 0.712 m/s^2 }[/math]
Question 2

Question:
A rabbit can jump to a height of 2.62 m. Determine the takeoff speed of the rabbit.
Solution:
Given:
- [math]\displaystyle{ a = -9.8 m/s^2 }[/math]
- [math]\displaystyle{ v_f = 0 m/s }[/math] *Considering the moment of takeoff to maximum height
- [math]\displaystyle{ d = 2.62 m }[/math]
Find:
- [math]\displaystyle{ v_i = ? }[/math]
Calculations:
- [math]\displaystyle{ v_f^2 = v_i^2 + 2ad }[/math]
- [math]\displaystyle{ v_i^2 = 2ad - v_f^2 }[/math]
- [math]\displaystyle{ v_i = \sqrt{2ad - v_f^2} }[/math]
- [math]\displaystyle{ v_i = \sqrt{2*-9.8m/s^2*2.62m - (0m/s)^2} }[/math]
- [math]\displaystyle{ v_i = 7.17 m/s }[/math]
Question 3

Question:
A rock is dropped into a lake and is heard to hit the water 3.41 s after being dropped. Determine the depth of the lake.
Solution:
Given:
- [math]\displaystyle{ a = -9.8 m/s^2 }[/math]
- [math]\displaystyle{ t = 3.41 s }[/math]
- [math]\displaystyle{ v_i = 0 m/s }[/math]
Find:
- [math]\displaystyle{ d = ? }[/math]
Calculations:
- [math]\displaystyle{ d = v_i*t + 0.5*a*t^2 }[/math]
- [math]\displaystyle{ d = (0 m/s)*(3.41 s)+ 0.5*(-9.8 m/s^2)*(3.41 s)^2 }[/math]
- [math]\displaystyle{ d = 0 m + 0.5*(-9.8 m/s^2)*(11.63 s^2) }[/math]
- [math]\displaystyle{ d = -57.0 m }[/math] (57.0 meters deep)