Energy of a Single Particle
Introduction
We are going to take a side step from the macroscopic world for a moment, and focus on the energy of very small particles - particles like protons, neutrons and electrons. Because of revolutions in modern physics in the last two centuries, we know that these particles act differently than objects in the macroscopic world - in fact, any object that can move close to the speed of light will behave differently than most objects we encounter in our daily life. Because of this, we need different ways of calculating the energy associated with them.
There are two types of energy these particles can have: rest energy and kinetic energy. Rest energy is, as you might expect, the energy of the rest mass of a particle. Kinetic energy, as we have seen before, is the energy associated with the motion of a particle. Calculations associated with these energies are usually very simple, so pay attention to the equations and units and you should be fine.
The formulas for calculating rest energy and kinetic energy may look familiar to you. That is because they are a lot like the formulas used to compute the energy of macroscopic quantities. The only main difference you may notice immediately is there is a γ (gamma) in those equations. That gamma is a Lorentz Factor, which is used to make relativistic corrections as a particle approaches the speed of light. You'll notice in the formula for gamma (shown below) that as the ratio of the particle speed to the speed of light approaches zero, γ approaches 1. Then, the formulas look exactly like the ones you are used to!
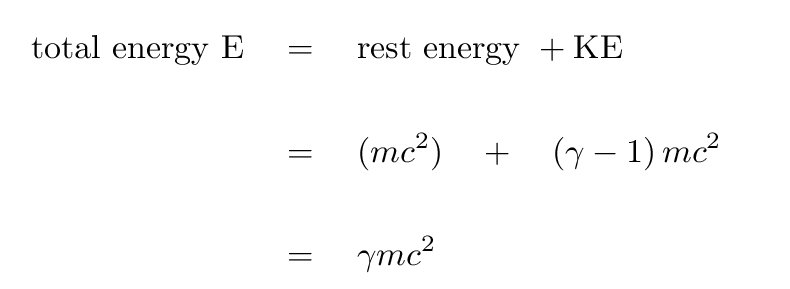
(see ref. 1)
A Mathematical Model
Types of point particles:
- 1. Electrons
- 2. Protons
- 3. Neutrons
Masses of point particles:
- 1. Electron mass = 9.109 e -31 kg
- 2. Proton mass = 1.6726 e -27 kg
- 3. Neutron mass = 1.6750 e -27 kg
There are three equations to look at that were discussed above:
(1) Relativistic Correction (Lorentz) Factor
[math]\displaystyle{ γ = \sqrt{1-(v/c)} }[/math] where v is the velocity of the particle and c is the speed of light
(2) Rest Energy of a particle
[math]\displaystyle{ E_{Rest}=mc^2 }[/math] - Rest Energy, where m is the mass and c is the speed of light. This type of energy describes the inherent energy contained within an object arising from chemical makeup. Rest energy will only ever change if the system being observed is at an atomic level where particles tends to change identities spontaneously during interactions with surroundings.
(3) Kinetic Energy of a particle nearing the speed of light
[math]\displaystyle{ E_{Kinetic}=γmc^2-mc^2 }[/math] - Where γ is as calculated above, m is the mass of the particle and c is the speed of light
(4) The combined energy equation
[math]\displaystyle{ E_{Particle}=γmc^2 }[/math]
Where γ is as calculated above, m is the mass of the particle and c is the speed of light
A Computational Model
ENTER COMPUTATIONAL MODEL INFO HERE
Examples
A proton moves at 0.950c.
Calculate its (a) rest energy, (b) total energy, and (c) kinetic energy.
- (a) [math]\displaystyle{ E_{rest}=mc^2 }[/math] = (1.67e-27 kg)(3e8 m/s)^2 = 1.5e-10 J
- (b) [math]\displaystyle{ E_{particle}=γmc^2 }[/math] = (1.5e-10 J)/((1-(0.950c/c)^2)^(1/2)) = 4.81e-10 J
- (c) [math]\displaystyle{ K=γmc^2-mc^2 }[/math] = 4.81e-10 J - 1.50e-10 J = 3.31e-10 J
An electron is accelerated to a speed of 2.95 × 108 (
a) What is the energy of the electron? (b) What is the rest energy of the electron? (c) What is the kinetic energy of the moving proton?
(a)
E = γmc2
E = (5.50)(9.11 × 10-31)(3 × 108)
E = 1.50 × 10-21 J
(b)
Erest = mc2
Erest = (9.11 × 10-31)(3 × 108)2
Erest = 2.73 × 10-22 J
(c)
K = E - Erest
K = 1.50 × 10-21 - 2.73 × 10-22
K = 1.23 × 10-21 J
Connectedness
ADD INFO ABOUT CONNECTEDNESS HERE
History
ADD HISTORY INFO HERE
More Info
(1) http://spiff.rit.edu/classes/phys150/lectures/ke_rel/ke_rel.html