Rotational Kinematics
Claimed by Aditya Kuntamukkula 2017
The Main Idea
Rotational Motion (also known as curvilinear motion), in contrast to linear ( also known as rectilinear) motion, involves motion of objects where the angular position of an object changes over time (For this reason, it is common practice to use polar coordinates when analyzing any object undergoing rotational motion). Because of this, rotational quantities are often called angular quantities, as they describe the angular component of an object's motion.
A Mathematical Model
Similar to linear motion, angular quantities can be described by a series of differential equations which relate the rate of change of a given quantity to some other aspect of rotational motion. These equations are listed below:
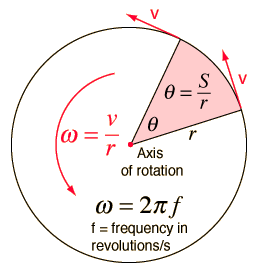
- [math]\displaystyle{ \boldsymbol{{\omega}} = \frac{d\boldsymbol{\theta}}{dt} }[/math]
- [math]\displaystyle{ \boldsymbol{{\alpha}} = \frac{d\boldsymbol{\omega}}{dt} }[/math]
- [math]\displaystyle{ \boldsymbol{{\alpha}} = \frac{{d}^{2}\boldsymbol{\omega}}{{dt}^{2}} }[/math]
Angular acceleration is equal to alpha:
- [math]\displaystyle{ \boldsymbol{{\alpha}} = \frac{\boldsymbol{a_t}}{\boldsymbol{r}} }[/math] ,
where [math]\displaystyle{ {\boldsymbol{a_t}} }[/math] is the tangential acceleration of the object and [math]\displaystyle{ {\boldsymbol{r}} }[/math] is the radius of the circle of motion.
Rotational Kinetic Energy:
An object with a center of mass at rest can still have rotational kinetic energy. For example, if a disk is suspended in the air and spun, it has no translational kinetic energy. The position of the disk does not change. However, since it is spinning (rotating), it still has kinetic energy. To account for this, we can relate angular velocity with the moment of inertia of the object to find a value for the rotational kinetic energy.
Rotational Kinetic Energy:
- [math]\displaystyle{ {KE}_{rot} = \frac{{1}}{{2}}{I}_{cm}{ω^2} }[/math]
Relation to Work and Energy Principle:
The energy principle states:
- [math]\displaystyle{ {E}_{f} = {E}_{i} + W }[/math]
We can apply the energy principle to rotational kinetic energy as well to find changes in kinetic energy and work done on the system.
Examples
Simple
A simple example and application of the concept of rotation is the earth's rotation on it's axis. It rotates once every 24 hours. What is the angular velocity?
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{d\theta}}{\boldsymbol{dt}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{\delta\theta}}{\boldsymbol{\delta t}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{2\pi}}{\boldsymbol{24}}\frac{\boldsymbol{rad}}{\boldsymbol{hr}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{\pi}}{\boldsymbol{12}}\frac{\boldsymbol{rad}}{\boldsymbol{hr}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{\pi}}{\boldsymbol{12}}\frac{\boldsymbol{rad}}{\boldsymbol{hr}}*\frac{\boldsymbol{1}}{\boldsymbol{3600}}\frac{\boldsymbol{hr}}{\boldsymbol{s}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{\pi}}{\boldsymbol{43200}}\frac{\boldsymbol{rad}}{\boldsymbol{s}} }[/math]
Angular velocity can also be represented as change in angle (theta) over change in time. In this case, the earth rotates 2pi radians in 24 hours which reduces to pi/12 rad/hr and that is the equivalent of pi/43200 rad/s.
Medium
A cylinder with a 2.5 ft radius is rotating at 120 rpm. Find the angular velocity in rad/sec. Find the linear velocity of a point on its rim in mph.
- [math]\displaystyle{ \boldsymbol{{w}} = {\boldsymbol{120}}\frac{\boldsymbol{rev}}{\boldsymbol{min}}*\frac{\boldsymbol{2\pi}}{\boldsymbol{1}}\frac{\boldsymbol{rad}}{\boldsymbol{rev}}*\frac{\boldsymbol{1}}{\boldsymbol{60}}\frac{\boldsymbol{min}}{\boldsymbol{s}} = {\boldsymbol{4\pi}}\frac{\boldsymbol{rad}}{\boldsymbol{s}} }[/math]
- [math]\displaystyle{ \boldsymbol{{v}} = {\boldsymbol{w}}{\boldsymbol{r}} }[/math]
- [math]\displaystyle{ \boldsymbol{{v}} = {\boldsymbol{4\pi}}\frac{\boldsymbol{rad}}{\boldsymbol{s}}*{\boldsymbol{2.5}}\frac{\boldsymbol{ft}}{\boldsymbol{rad}} = {\boldsymbol{10\pi}}\frac{\boldsymbol{ft}}{\boldsymbol{s}} }[/math]
- [math]\displaystyle{ \boldsymbol{{v}} = {\boldsymbol{10\pi}}\frac{\boldsymbol{ft}}{\boldsymbol{s}}*\frac{\boldsymbol{3600}}{\boldsymbol{1}}\frac{\boldsymbol{s}}{\boldsymbol{hr}}*\frac{\boldsymbol{1}}{\boldsymbol{5280}}\frac{\boldsymbol{miles}}{\boldsymbol{ft}} =\frac{\boldsymbol{75\pi}}{\boldsymbol{11}}\frac{\boldsymbol{miles}}{\boldsymbol{hr}} }[/math]
To find the solution of this problem, rpm (revolutions per minute) should be converted to radians/second. Following this, the linear velocity can be calculated by using the v=wr formula shown above. The angular velocity is 4pi radians per second and the linear velocity is 75pi/11 or 21.42 mph.
Difficult
A tire with a 9 inch radius is rotating at 30 mph. Find the angular velocity at a point on its rim. Also express the result in revolutions per minute.
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{v}}{\boldsymbol{r}} }[/math]
- [math]\displaystyle{ \boldsymbol{{r}} = {\boldsymbol{9}}{\boldsymbol{in}}*\frac{\boldsymbol{1}}{\boldsymbol{12}}\frac{\boldsymbol{ft}}{\boldsymbol{in}}*\frac{\boldsymbol{1}}{\boldsymbol{5280}}\frac{\boldsymbol{miles}}{\boldsymbol{ft}} = \frac{\boldsymbol{1}}{\boldsymbol{7040}}{\boldsymbol{miles}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{30}}{\frac{\boldsymbol{1}}{\boldsymbol{7040}}}\frac{\frac{\boldsymbol{miles}}{\boldsymbol{hr}}}{\frac{\boldsymbol{rad}}{\boldsymbol{miles}}} = \boldsymbol{{211200}\frac{\boldsymbol{rad}}{\boldsymbol{hr}}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \boldsymbol{{211200}\frac{\boldsymbol{rad}}{\boldsymbol{hr}}}*\frac{\boldsymbol{1}}{\boldsymbol{2\pi}}\frac{\boldsymbol{rev}}{\boldsymbol{rad}}*\frac{\boldsymbol{1}}{\boldsymbol{60}}\frac{\boldsymbol{hr}}{\boldsymbol{min}} = \frac{\boldsymbol{1760}}{\boldsymbol{\pi}}\frac{\boldsymbol{rev}}{\boldsymbol{min}} }[/math]
Connectedness
Rotation is an extremely important aspect of dynamics (the study of moving objects) which plays a big role in biomechanics. Rotation relates to several important body parts such as the shoulder where there are two axis of rotation, the medial-lateral axis and the anterior-posterior axis. A study of the movement of the shoulder helps to treat medical conditions that may affect this area. Dynamics is also very important in many other disciples, including mechanical engineering and aerospace engineering.
See also
To learn more about Rotation in a more complete context, please refer to Torque or Rigid-Body Objects or Angular Momentum.
Further reading
Books, Articles or other print media on this topic
External links
Some other resources to further understand rotation are the following:
http://www.mathwarehouse.com/transformations/rotations-in-math.php
http://demonstrations.wolfram.com/Understanding3DRotation/
References
[1] Biomechanics, Basic. “It Is Important When Learning about (n.d.): n. pag. Web.
[2] "Angular Velocity and Angular Acceleration." Van Nostrand's Scientific Encyclopedia (2005): n. pag. Web