Curving Motion

Main Idea

In the previous section, we introduced the idea of conservation of momentum. By choosing multiple particles as the system, we can assume that the forces exerted by the particles in the system are reciprocal of one another, based on Newton's Third Law of Motion. The total change in momentum is zero if the system's forces all canceled out and no forces in the surrounding are acting on the system. This special case, where the momentum of the system remains constant ([math]\displaystyle{ \Delta p = 0 }[/math]), can be implicated in many situations that helps us to identify forces exerted on the system. However, in the case when the momentum of the system changes with time, which means velocity and/or direction of motion are nonconstant and additional terms are needed to define the magnitude and direction of the momentum of the objects in the system. The momentum of an object is nonconstant when it is traveling along a curved path, regardless of whether or not it's speed along the curve is changing because the direction also changes. Curving motion can be analyzed using the properties of the parallel and perpendicular components of net Force ([math]\displaystyle{ F_{net} }[/math]) as well as understanding the motion's "Kissing Circle".

Mathematical Model

Parallel and Perpendicular Forces

The parallel force lies along the direction of the momentum vectors and is calculated as [math]\displaystyle{ \mathbf{F_{\parallel}} = |\mathbf{F_{net}}| \text{cos}(\theta) \ \mathbf{\hat p} }[/math]. Since [math]\displaystyle{ \mathbf{F_{net}} }[/math] is the sum of its parallel and perpendicular components, [math]\displaystyle{ \mathbf{F_{\perp}} }[/math] can be obtain simply by taking the difference between the two: [math]\displaystyle{ \mathbf{F_{\perp}} = \mathbf{F_{net}} - \mathbf{F_{\parallel}} = \mathbf{F_{net}} - |\mathbf{F_{net}}|\text{cos}(\theta) \ \mathbf{\hat p} }[/math]

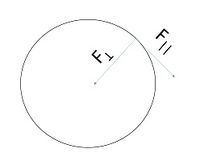
The image above describes a particle moving in a clockwise circular motion. Note that [math]\displaystyle{ \mathbf{F_\perp} }[/math] always points inward for a circular path. [math]\displaystyle{ \mathbf{F_\parallel} }[/math] gives the change in magnitude of the object's momentum, and [math]\displaystyle{ \mathbf{F_\perp} }[/math] gives the change in direction of the object's momentum.

Understanding the Components of [math]\displaystyle{ \frac{d\mathbf{p}}{dt} }[/math]

When the change in momentum with respect to time is nonzero, we will consider both the parallel and perpendicular components of momentum, and their relationship to the net force. If an object is speeding up or slowing down, [math]\displaystyle{ \frac{d \mathbf{p}}{dt}_{\parallel} \ne 0 }[/math]. If an objects is turning while traveling along a path, [math]\displaystyle{ \frac{d\mathbf{p}}{dt}_{\perp} \ne 0 }[/math]. The parallel component accounts for the change in speed of the motion, while the perpendicular component accounts for the change in direction of the motion. Here is a list of useful formulas:

[math]\displaystyle{ \frac{d\mathbf{p}}{dt} = \frac{d\mathbf{p}}{dt}_\parallel + \frac{d\mathbf{p}}{dt}_\perp }[/math]

[math]\displaystyle{ \mathbf{F_{net}} = \mathbf{F_\parallel} + \mathbf{F_\perp} }[/math]

[math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\parallel = \frac{d|\mathbf{p}|}{dt} \mathbf{\hat p} = \mathbf{F_\parallel} }[/math] (Change in magnitude of momentum)

[math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\perp = \frac{d\mathbf{\hat p}}{dt} |\mathbf{p}| = \mathbf{F_\perp} }[/math] (Change in direction of momentum)

[math]\displaystyle{ \mathbf{F_{net}} = \frac{d\mathbf{p}}{dt} = \frac{d|\mathbf{p}|}{dt} \mathbf{\hat p} + \frac{d\mathbf{\hat p}}{dt} |\mathbf{p}| }[/math]

Perpendicular Component and the Kissing Circle

The perpendicular component of momentum can be evaluated further so that it becomes:

[math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\perp = \frac{d\mathbf{\hat p}}{dt} |\mathbf{p}| = |\mathbf{p}| \frac{|\mathbf{v}|}{R} \mathbf{\hat n} = \frac{mv^2}{R} \mathbf{\hat n} }[/math]

The term [math]\displaystyle{ |\mathbf{p}| \frac{|\mathbf{v}|}{R} \mathbf{\hat n} }[/math] can be understood by drawing an imaginary circle, that touches or 'kisses' some point on a curved path, to represent the instantaneous curvature of an object's trajectory, where [math]\displaystyle{ R }[/math] is the radius of the circle. For a smooth, continuous curving motion, [math]\displaystyle{ \frac{|\mathbf{v}|}{R} }[/math] tells us the degree of which the object is turning and the rate of change of direction,[math]\displaystyle{ \frac{d\mathbf{\hat p}}{dt} }[/math]. The 'Kissing Circle' indicates the direction of the perpendicular component of momentum, which points towards the center of the kissing circle and it's denoted by [math]\displaystyle{ \mathbf{\hat n} }[/math].

Parallel Component and Tangential Properties of Curving Motion

The parallel component of momentum always points in the direction of motion, denoted by [math]\displaystyle{ \mathbf{\hat p} }[/math] and is tangent to the path of motion. The term [math]\displaystyle{ \frac{d|\mathbf{p}|}{dt} }[/math] describes the change in velocity of the objects with respect to time (since [math]\displaystyle{ \mathbf{p} = m\mathbf{v} }[/math]), and it corresponds to the change in the magnitude of the momentum.

There are two scenarios of curving motion that we will entertain here; one where an object is not changing speed along its curved path, and another where the object speeds up or slows down along its curved path. We will start with the constant speed scenario:[math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\parallel = 0 }[/math]

When an object's tangential velocity is constant throughout the entire motion, we can say that the parallel component of [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}} }[/math] is zero, as any change in momentum is solely from altering the direction of the object's momentum as opposed to its magnitude. To understand this in more mathematical terms, the only way the magnitude of a momentum vector can be changed is if some component of the force acting on the object lies in the direction of the objects motion. Otherwise, the net force must be in the perpendicular direction towards the center of the kissing circle, like shown below:

Kissing Circle

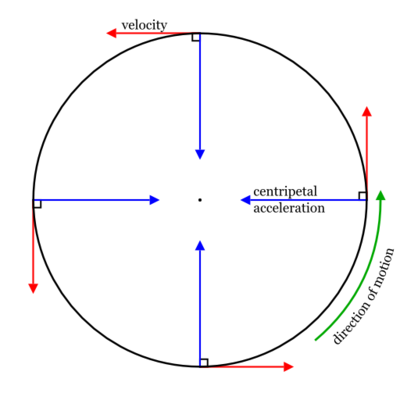
Here we see that the tangential velocities indicated by the red arrows are all of the same magnitude, and the only thing altering them is the centripetal acceleration, which will lead us into our discussion of centripetal and centrifugal forces in the next section. Now we will consider cases where [math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\parallel }[/math] is nonzero. In these cases, the speed of the object along its curved path is changing, and our net force vector has a component that is parallel to the object's tangential motion.

Calculating [math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\parallel }[/math] and [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}}_\perp }[/math] is possible, given an instantaneous force acting on the object as well as it's initial momentum. We can calculate the final momentum using the Momentum Principle, and then observe any change in magnitude between these two vector quantities. Here, [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}}_\parallel }[/math] is equal to the difference between the magnitudes of the initial and final momentum divided by the change in time. From this, we can calculate [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}}_\perp }[/math] by subtracting [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}}_\parallel }[/math] from the net change in momentum.

Computational Model

The parallel and perpendicular components of [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}} }[/math] can be modeled computationally using VPython. The code below models a situation in which a space craft interacts with the Earth and the Moon.

https://trinket.io/glowscript/f53cc1fa35

In this model, gravitational forces affect the motion of the space craft, causing it to curve in proportion to the perpendicular and parallel components of force. The yellow arrow following the craft's position shows the parallel component of force, and the magenta arrow shows the perpendicular component of force. Aspects of the code that account for these calculations are explained below:

The parallel component of force is calculated from the expression [math]\displaystyle{ {\frac{d|\mathbf{p}|}{dt}} \mathbf{\hat p} }[/math]

p_init = sqrt(pcrafti.x**2+pcrafti.y**2)

p_final = sqrt(pcraft.x**2+pcraft.y**2)

Fnet_tangent = ((p_final-p_init)/deltat)*(pcrafti)/(p_init)

The perpendicular component of force is calculated from the expression [math]\displaystyle{ \mathbf{F_{net}} = \mathbf{F_\parallel} + \mathbf{F_\perp} }[/math].

From this expression, it is seen that [math]\displaystyle{ \mathbf{F_{net}} - \mathbf{F_\parallel} = \mathbf{F_\perp} }[/math]

The computational model uses this insight, and the net force calculated earlier in the code to find the perpendicular component of net force.

Fnet_perp = Fnet - Fnet_tangent

To see the affects of the gravitational force on curving motion, you are encouraged to make changes to the initial values of the code and see the effects on the perpendicular and parallel components of force. These initial values can be edited in the beginning of the code in this section:

CONSTANTS G = 6.7e-11

mEarth = 6e24

mcraft = 15e3

mMoon = 7

deltat = 60

Fscale = 2e3

pscale = 1e-1

dpscale = 33

OBJECTS AND INITIAL VALUES

Earth = sphere(pos=vector(0,0,0), radius=6.4e6, color=color.cyan)

craft = sphere(pos=vector(-72960000,5248000,0), radius=1e5, color=color.yellow)

vcraft = vector(692,2950,0)

pcraft = mcraft*vcraft

moon = sphere(pos=vector(4e8,0,0), radius = 1.75e6, color=color.white)

moon.v = vector(0,sqrt((G*mEarth)/mag(moon.pos-Earth.pos)),0)

momentum_Moon = mMoon*moon.v

Examples

Simple

It's fairly simple identifying cases of curving motion, in which case a person can easily apply [math]\displaystyle{ {\frac{m v^{2}}{R}} }[/math] to a situation immediately. For example, if an object is traveling in a circular path at a constant speed, we can neglect the parallel component of [math]\displaystyle{ \frac{d\mathbf{p}}{dt} }[/math] and [math]\displaystyle{ \mathbf{F_{net}} }[/math], and consider only the perpendicular components, such as tension, gravitational, and contact forces.

Example:

A child whose mass is [math]\displaystyle{ 30 \ \text{kg} }[/math] sits on a merry-go-round at a distance of [math]\displaystyle{ 3 \ \text{meters} }[/math] from the center. The merry-go-round makes one revolution every [math]\displaystyle{ 8 \ \text{seconds} }[/math]. What are the magnitude and direction of the net force ([math]\displaystyle{ F_{net} }[/math]) acting on the child?

Solution:

We know that the net force acting on the child is the sum of the perpendicular force ([math]\displaystyle{ F_\perp }[/math]) and the parallel force ([math]\displaystyle{ F_\parallel }[/math]), so it is best to solve for each separately and then add them together.

Parallel:

Since the child moves at a constant speed, we know that [math]\displaystyle{ {\frac{d\mathbf{p}}{dt}}_\parallel }[/math] is 0:

[math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\parallel = \mathbf{F_\parallel} = \mathbf{0} }[/math]

Perpendicular:

We know that:

[math]\displaystyle{ |\mathbf{F_\perp}| = {\frac{m v^{2}}{R}} }[/math].

In this case (no parallel force, and thus circular motion):

[math]\displaystyle{ v = \frac{\text{Circumference of Circle}}{\text{Period}} = \frac{2 \pi \times R}{T} = \frac{2 \pi \times 3}{8} = 2.36 \ \frac{m}{s} }[/math], where:

[math]\displaystyle{ R = 3 \ \text{meters} }[/math]

[math]\displaystyle{ T = 8 \ \text{seconds} }[/math]

Therefore:

[math]\displaystyle{ |\mathbf{F_\perp}| }[/math] = [math]\displaystyle{ {\frac{(30)(2.36)^{2}}{3}} = 55.5 \ \text{Newtons} }[/math]

Net Force:

[math]\displaystyle{ \mathbf{F_{net}} = \mathbf{F_\parallel} + \mathbf{F_\perp} = 0 + \mathbf{F_\perp} }[/math]

Since [math]\displaystyle{ \mathbf{F_\perp} }[/math] is the only component of the net force, we know that [math]\displaystyle{ |\mathbf{F_{net}}| = 55.5 \text{Newtons} }[/math]. This net force is pointing in the perpendicular direction, towards the center of the merry-go-round.

Middling

Occasionally, it can be difficult to gauge any components that influence the object's tangential velocity and effectively speed up or slow down the object by altering the magnitude of the momentum vector.

Example:

Tarzan, whose mass is [math]\displaystyle{ 85 \ \text{kg} }[/math], is hanging from a vine that is [math]\displaystyle{ 8 \ \text{meters} }[/math] long. At the instant when he makes a [math]\displaystyle{ 40^\text{o} }[/math] angle between the vine and the vertical, he is traveling at a speed of [math]\displaystyle{ 13.4 \ \frac{m}{s} }[/math].

a) What is the rate of change of the magnitude of Tarzan's momentum?

First, we draw a free body diagram for Tarzan:

INSERT FBD

We know the magnitude of the change of momentum is related to the net parallel force by: (See Understanding the Components of [math]\displaystyle{ \frac{d\mathbf{p}}{dt} }[/math])

[math]\displaystyle{ \frac{d\mathbf{p}}{dt}_\parallel = \frac{d|\mathbf{p}|}{dt} \mathbf{\hat p} = \mathbf{F_\parallel} }[/math]

Taking the magnitude of each part of the equations gives:

[math]\displaystyle{ \left|\frac{d\mathbf{p}}{dt}_\parallel\right| = \frac{d|\mathbf{p}|}{dt} = |F_\parallel| }[/math]

The only force acting in the parallel direction to the momentum of Tarzan is the parallel component of the gravitational force:

[math]\displaystyle{ |\mathbf{F_\parallel}| = |\mathbf{F_g}| \text{cos}(90^\text{o} - 40^\text{o}) = |\mathbf{F_g}| \text{cos}(50^\text{o}) }[/math]

The magnitude of the gravitational force is just:

[math]\displaystyle{ |\mathbf{F_g}| = mg }[/math], where

[math]\displaystyle{ m = 85 \ \text{kg} }[/math] (Mass of Tarzan)

[math]\displaystyle{ g = 9.81 \ \frac{m}{s^2} }[/math] (Acceleration due to gravity)

Therefore:

[math]\displaystyle{ \frac{d|\mathbf{p}|}{dt} = 85 \times 9.81 \times \text{cos}(50^\text{o}) = 536 \ \frac{\text{kg m}}{\text{s}^2} }[/math]

b) What is the tension in the vine?

Finding the tension in the vine can be done in the easiest way by looking at the component of the net force perpendicular to the momentum. We know that:

[math]\displaystyle{ \mathbf{F_\perp} = \frac{d\mathbf{p}}{dt}_\perp = \frac{mv^2}{R} \mathbf{\hat n} }[/math], where

[math]\displaystyle{ m = 85 \ \text{kg} }[/math] (Mass of Tarzan)

[math]\displaystyle{ v = 13.4 \ \frac{m}{s} }[/math] (Speed at this point in time)

[math]\displaystyle{ R = 8 \ \text{meters} }[/math] (Length of the vine)

Taking the magnitude of each side we see that:

[math]\displaystyle{ |\mathbf{F_\perp}| = \frac{mv^2}{R} }[/math]

The forces acting on Tarzan along the perpendicular axis are the perpendicular component of gravity ([math]\displaystyle{ |\mathbf{F_g}| \text{sin}(\phi) }[/math]) and the force of tension ([math]\displaystyle{ |\mathbf{F_T}| }[/math]). Using this fact we can set up these equations:

[math]\displaystyle{ |\mathbf{F_\perp}| = \frac{mv^2}{R} = |\mathbf{F_T}| - |\mathbf{F_g}| \text{sin}(\phi) }[/math]

Therefore:

[math]\displaystyle{ |\mathbf{F_T}| = \frac{mv^2}{R} + |\mathbf{F_g}| \text{sin}(\phi) }[/math]

By using some right triangle trigonometry, we find [math]\displaystyle{ \phi }[/math] to be [math]\displaystyle{ 50^\text{o} }[/math]. We also note that the magnitude of the gravitational force is [math]\displaystyle{ mg }[/math], where [math]\displaystyle{ g \ \text{is} \ 9.81 \frac{m}{s^2} }[/math].

Plugging in values gives:

[math]\displaystyle{ |\mathbf{F_T}| = \frac{85 \times (13.4)^2}{8} + 85 \times 9.81 \times \text{sin}(50^\text{o}) }[/math]

Which gives:

[math]\displaystyle{ |\mathbf{F_T}| = 2546.6 \ \text{Newtons} }[/math]

Difficult

It can be fairly difficult to understand when there are other factors that influence the perpendicular component of the change of momentum, or when an individual needs to identify another influential force in that axis. For instance, in the Ferris Wheel example, when asked about having to find the necessary velocity for the rider to feel weightless, the individual needs to understand that there's a surface contact force that is also in play and in this case needs to be 0, in which case gravitational force is equal to [math]\displaystyle{ {\frac{m v^{2}}{R}} }[/math].

If a person on the Ferris Wheel is not positioned on the x- or y-axis, we cannot assume that the gravitational and contact forces are acting the same way as when the person is sitting on the Cartesian coordinate system. The reason we chose this coordinate system is because it coincides with the directions of the parallel and perpendicular forces. A oriented coordinates system must be created to accommodate this change and it will be aligned with [math]\displaystyle{ \hat n }[/math] and [math]\displaystyle{ \hat p }[/math].

Example: A Ferris Wheel has a radius r and rotates counter-clockwise with a constant angular rate ω. A person with mass m is riding in the gondola at an angle of θ = 40◦ from the x-axis as shown. What is the magnitude of the parallel and perpendicular components of the contact forces?

Problem worked out in the video below:

https://youtu.be/M5ISjDc5tSc

Connectedness

1. How is this topic connected to something that you are interested in?

Curving motion is heavily employed when observing planetary orbits, something I find highly fascinating. Although in reality these orbits aren't perfectly circular as we often make them out to be, they still heavily demonstrate the ideas of curving motion and especially [math]\displaystyle{ {\frac{m v^{2}}{R}} }[/math]!

1. How is it connected to your major?

As of now I am a CS major, and using vPython to model curving motion animations among many things helps apply programming ideas such as iteration and variable update.

1. Is there an interesting industrial application?

Centripetal and Centrifugal forces can be found in many industrial applications, as curved motion is a very frequent occurrence when observing interactions between various objects. For instance, a centrifuge using these mechanics helps astronauts train for higher effective gravity.