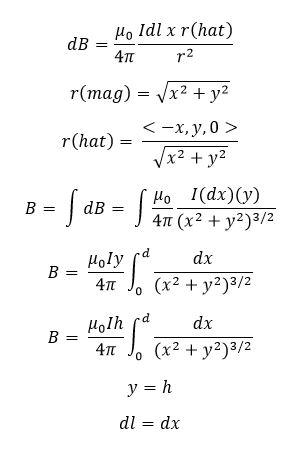Integration Techniques for Magnetic Field
In the study of magnetic fields, many formulas for the magnetic field of different objects are derived by integrating the magnetic field of a small portion of the object over the entire area of the object. Often times, you will also be expected to derive your own formulas for less common shapes.
The Main Idea
All integration for magnetic fields is based on the Biot-Savart Law for currents, which is 
. First, you will take a small portion of the object and call its position Δl. Then find the unit vector from this point to the observation location. Then, take the cross-product of these two vectors and you should end up with a vector that only exists in one dimension (x, y, or z). Now set up your integral by first taking out all the constants from the equation and putting them outside the integral. This should be your mu(naught)/4(pi) and your current. Inside the integral, keep the cross product of the two vectors over r^2, as those are the values that can change during integration. Then set up your limits of integration by going over the full area/length of the object. For example, if you have a rod, integrate over the length of the rod. If you have a loop, integrate from 0 to 2(pi) for the full area of the loop.
Mathematical Model
and then 
Computational Model
This is code from a previous lab that simulates a moving proton creating a magnetic field. Because current creates magnetic field and current is essentially a moving charge, this model helps you to see that the location of the moving charge in relation to the observation location changes the magnitude of the magnetic field. As a result, it is important to consider all the points of a wire and thus all the different locations of a moving charge when finding the net magnetic field of a wire. For this reason, we use integration to find net magnetic field.
from __future__ import division
from visual import *
- Constants
oofpez = 1e-7
qproton = (-1.6e-19)
- Objects
- Change the initial vector position of the proton below:
proton = sphere(pos=vector(3e-10,0,0), radius=1e-11, color=color.red)
- Change the observation location (position of the tail of the arrow) below:
- Add more arrows to find magnetic field at other observation locations.
- Set axis to (0,0,0) initially and update it in the loop.
barrow1=arrow(pos=vector(0,8e-11,0), axis=vector(0,0,0), color=color.cyan)
barrow2=arrow(pos=vector(0,-8e-11,0), axis=vector(0,0,0), color=color.cyan)
barrow3=arrow(pos=vector(0,0,8e-11), axis=vector(0,0,0), color=color.cyan)
barrow4=arrow(pos=vector(0,0,-8e-11), axis=vector(0,0,0), color=color.cyan)
- Initial values
velocity = vector(-5.2e4,0,0) # Enter the proton's velocity
deltat = 1e-17 # Adjust if program runs too slowly or too quickly
scene.autoscale=0 #Turns off autoscaling. Set to 1 to turn it back on.
- Loop
while proton.x<5e-10:
rate(100) # For each magnetic field vector: # 1. Calculate r and rhat r1 = barrow1.pos - proton.pos r2 = barrow2.pos - proton.pos r3 = barrow3.pos - proton.pos r4 = barrow4.pos - proton.pos
r1hat = norm(r1) r2hat = norm(r2) r3hat = norm(r3) r4hat = norm(r4)
r1mag = mag(r1) r2mag = mag(r2) r3mag = mag(r3) r4mag = mag(r4) # 2. Calculate the magnetic field vector
B1 = (oofpez)*(qproton)*((cross(velocity,r1hat))/(r1mag**2)) B2 = (oofpez)*(qproton)*((cross(velocity,r2hat))/(r2mag**2)) B3 = (oofpez)*(qproton)*((cross(velocity,r3hat))/(r3mag**2)) B4 = (oofpez)*(qproton)*((cross(velocity,r4hat))/(r4mag**2)) # 3. Calculate the new axis of the arrow. Scale it appropriately.
barrow1.axis = 5e-9*B1 barrow2.axis = 5e-9*B2 barrow3.axis = 5e-9*B3 barrow4.axis = 5e-9*B4
# Update the proton's position proton.pos += velocity * deltat
Example
Simple
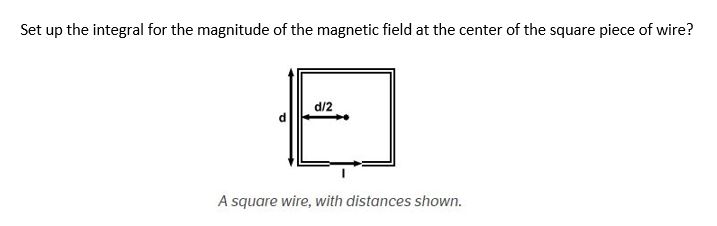
Middling
Hard
Connection
Calculus was invented to do physics. By integrating over an object to find its magnetic field, you are performing one of the basic operations on which physics is founded on, which is used to derive other formulas. Additionally, using this method should allow you to find the magnetic field of any object, no matter its shape or size.