by Jong Rak Koh

Overview

Leonhard Euler was a Swiss Mathematician and physicist who made important contributions to math and physics. Euler is often considered one of the greatest mathematicians to have ever lived.

Early Life

Euler was born in Basel, Switzerland on April 15th, 1707. His father was a minister and the family naturally expected Euler to also go in to ministry. However, his father sparked a curiosity in math for Euler and Euler entered University of Basel at the age of 14, with Johann Bernoulli as his mentor.

Contributions to Physics

Arguably the greatest mathematician in history, Euler made lots of contribution to math such as the number “e”, the concept of a function, summation notation “[Sigma|Σ]”, imaginary unit notation “Template loop detected: Template:Math”, and popularizing “<ref name="pi">”; however, Euler also made lots of important contributions to physics.

Euler-Bernoulli beam equation

The theory validates the beam deflection calculation for laterally loaded beams. The equation provides a relationship between the deflection of the beam and the applied load intensity.

Work in Astronomy

Understanding the nature of comets

In addition to his work with classical mechanics, Euler was recognized by Paris Academy Prizes over the course of his career for calculating, with great accuracy, the orbits of comets and other celestial bodies.

Calculating the parallax of the sun

Euler calculated the parallax of the sun, calculating the difference in the apparent position of the object and the actual position of the object. Euler’s calculation of the parallax later led to the development of more accurate longitude tables.

Work in optics

While Newton argued that light was made of particles, Euler argued that light behaved more like waves. In Nova theoria lucis et colorum (1746), Euler argued that diffractions can be more easily argued with the wave theory rather than the previous “pulse theory”. Euler’s wave theory remained the dominant theory about light until the quantum theory of light.

Structural Engineering

Euler also published a formula for calculating the force where the strut would fail that is often used in structural engineering.

Fluid Dynamics

Euler in 1757 published a set of equations for flow of an ideal fluid with no viscosity (Inviscid flow) that are now known as the Euler Equations.

[math]\displaystyle{ \rho\left( \frac{\partial}{\partial t}+{\bold u}\cdot\nabla \right){\bold u}+\nabla p=0 }[/math]

Simple Example

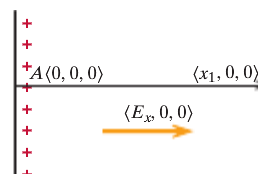
In this example, the electric field is equal to [math]\displaystyle{ E = \left(E_x, 0, 0\right) }[/math]. The initial location is A and the final location is C. In order to find the potential difference between A and C, we use [math]\displaystyle{ dV = V_C - V_A }[/math].

Since there are no y and z components of the electric field, the potential difference is [math]\displaystyle{ dV = -\left(E_x*\left(x_1 - 0\right) + 0*\left(-y_1 - 0\right) + 0*0\right) = -E_x*x_1 }[/math]

Let's say there is a location B at [math]\displaystyle{ \left(x_1, 0, 0\right) }[/math]. Now in order to find the potential difference between A and C, we need to find the potential difference between A and B and then between B and C.

The potential difference between A and B is [math]\displaystyle{ dV = V_B - V_A = -\left(E_x*\left(x_1 - 0\right) + 0*0 + 0*0\right) = -E_x*x_1 }[/math].

The potential difference between B and C is [math]\displaystyle{ dV = V_C - V_B = -\left(E_x*0 + 0*\left(-y_1 - 0\right) + 0*0\right) = 0 }[/math].

Therefore, the potential difference A and C is [math]\displaystyle{ V_C - V_A = \left(V_C - V_B\right) + \left(V_B - V_A\right) = E_x*x_1 }[/math], which is the same answer that we got when we did not use location B.

Connectedness

How is this topic connected to something that you are interested in?
How is it connected to your major?
Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

Leonhard Euler

Contents