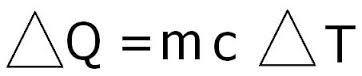Specific Heat Capacity
by Dejan Tojcic
Specific Heat Capacity
Specific Heat Capacity is simply a physical quantity that represents the ratio of the amount of heat taken or added to substance or object which results in a temperature change. The formal definition of Specific Heat is the amount of heat required to raise the temperature of 1 gram of a substance 1°C. The Standard Unit(SI) of this quantity is, joule per celsius per kilogram or or [math]\displaystyle{ \mathrm{\tfrac{J}{°C*Kg}} }[/math]. Different objects/substances have different specific heat capacities because every object has a varying mass, molecular structure, and numbers of particles per unit mass specific, and since specific heat capacity is reliant on mass, every different object has a different specific heat capacity.
A Mathematical Model
In order to find the Specific Heat Capacity of a substance, we use the equation:[math]\displaystyle{ \Delta E_{\mathrm{thermal}} = C * M * \Delta T }[/math], and rearrange it to get [math]\displaystyle{ C= \Delta E_{\mathrm{thermal}} /( M * \Delta T) . }[/math] where C is the Specific Heat Capacity with units of joules per celsius per kilogram or [math]\displaystyle{ \mathrm{\tfrac{J}{°C*Kg}} }[/math], M is the mass measured in kilograms or [math]\displaystyle{ \mathrm{kg} }[/math], [math]\displaystyle{ \Delta E_{\mathrm{thermal}} }[/math] represents the change in thermal energy measured by joules or [math]\displaystyle{ \mathrm{J} }[/math], and [math]\displaystyle{ \Delta T }[/math] represents change in temperature with units celsius or [math]\displaystyle{ \mathrm{°C.} }[/math]
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
Simple Example
Question It takes 487.5 J to heat 25 grams of copper from 25 °C to 75 °C. What is the specific heat in Joules/g·°C?
Solution
This problem is very simplistic in nature as we are simply need to plug all of the values into the equation. Remembering the equation
All we have to do is rearrange it and solve for the specific heat capacity
Knowing that [math]\displaystyle{ \ Q }[/math] or [math]\displaystyle{ \Delta E_{\mathrm{thermal}} }[/math] is equal to the change in thermal energy, we can plug in 487.5 Joules into the equation, so now we have
[math]\displaystyle{ C= 487.5 joules /( M * \Delta T) . }[/math]
Next, looking at the question it looks like we are given the mass or [math]\displaystyle{ \mathrm{M} }[/math] which is 25 grams or . And can now plug that into the equation to get
[math]\displaystyle{ C= 487.5 joules /(25g * \Delta T) . }[/math]
Lastly, when we read the problem we see that we are given [math]\displaystyle{ \Delta T }[/math] which in this case would be [math]\displaystyle{ (75 °C-25 °C) }[/math] or [math]\displaystyle{ 50 °C }[/math]. We can finally solve for the value of [math]\displaystyle{ \mathrm{C} }[/math] which is
[math]\displaystyle{ C= 487.5 joules /( 25g * 50 °C) . }[/math]
and we finally conclude that
[math]\displaystyle{ C= .39{\tfrac{J}{g*°C}} }[/math] or the specific heat of copper is .39 J/(g*°C).
Intermediate example
Question What is the final temperature when 625 grams of water at 75.0° C loses 7.96 x 10^4 J?
Solution While this problem may seem impossible at first glance, it really is not. It appears as if we are missing two constants,[math]\displaystyle{ \Delta T }[/math] and [math]\displaystyle{ C }[/math], or change in temperature and specific heat capacity. Water's specific heat capacity is almost "a universal constant" as it is noted for being the highest out of all substances with the value of 4.18 joules/(grams* °C). Now knowing the value [math]\displaystyle{ C=4.18{\tfrac{J}{°C*g}} }[/math], we see that the question is asking for [math]\displaystyle{ \Delta T }[/math], which is equal to [math]\displaystyle{ ( T_{\mathrm{initial}} - T_{\mathrm{final}}) }[/math].
We can again use the same equation as on this occasion we are solving for [math]\displaystyle{ \Delta T }[/math] or [math]\displaystyle{ ( T_{\mathrm{final}}) }[/math] more specifically, so we can rearrange it to get
[math]\displaystyle{ \Delta T= \Delta E_{\mathrm{thermal}}/( C * M) }[/math]
We can start plugging in variables now, so we know [math]\displaystyle{ \Delta E_{\mathrm{thermal}}=7.96 * 10^4 J }[/math], and we know this because in the problem it states "loses 7.96 x 10^4 J? Therefore the equation now looks like
[math]\displaystyle{ \Delta T= 7.96 x 10^4 J/( C * M) }[/math]
We can now plug in the mass of the water as in the problem it was given to be [math]\displaystyle{ M= 625 grams }[/math] as now the updated equation is
[math]\displaystyle{ \Delta T= 7.96 x 10^4 J/( C * 625 grams) }[/math]
Lastly, all we need to add to calculate [math]\displaystyle{ \Delta T }[/math] is ,[math]\displaystyle{ C }[/math], which is the specific heat capacity for water commonly known to equal [math]\displaystyle{ C=4.18{\tfrac{J}{°C*g}} }[/math].
[math]\displaystyle{ \Delta T= 7.96 x 10^4 J/( 4.18{\tfrac{J}{°C*g}} * 625 grams) }[/math]
We have finally solved the equation and determined that
[math]\displaystyle{ \Delta T= 30.5°C }[/math]
However, if you look at the question, it asks for "final temperature" and not [math]\displaystyle{ \Delta T }[/math]. Thus in order to calculate the final temperature we must use the equation [math]\displaystyle{ \Delta T= T_{\mathrm{initial}} - T_{\mathrm{final}} }[/math] and rearrange it to solve for [math]\displaystyle{ T_{\mathrm{final}} }[/math] so that it looks like
[math]\displaystyle{ T_{\mathrm{final}}= T_{\mathrm{initial}}-\Delta T }[/math]
And since the quantities [math]\displaystyle{ T_{\mathrm{initial}}= 75.0°C }[/math] and [math]\displaystyle{ \Delta T= 30.5°C }[/math] are known, we simply plug these into the formula to compute [math]\displaystyle{ T_{\mathrm{final}} }[/math]
[math]\displaystyle{ T_{\mathrm{final}}= 75.0°C- 30.5°C }[/math]
So we finally determine that [math]\displaystyle{ T_{\mathrm{final}}= 44.5°C }[/math].
Hard Example
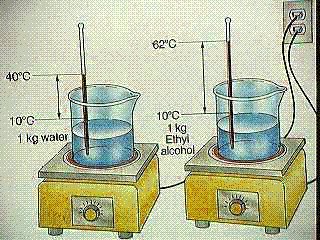
Question Calculate the specific heat of ethyl alcohol using the diagram
Analyze the problem: You need to look into the diagram pretty deeply before you attempt to to solve the problem. The question directly states that it is looking for the specific heat of the ethyl alcohol, but that is all it says so we will need to analyze the diagram itself.
Looking at the diagram we can see that there is 1 kilograms or 1000 grams of ethyl alcohol, so we know [math]\displaystyle{ \mathrm{M}= 1000grams }[/math] .
Next when solving for [math]\displaystyle{ \Delta T_{\mathrm{ethyl alcoholl}} }[/math] we can see in the diagram that they give us the initial temperature of [math]\displaystyle{ T_{\mathrm{initial}}= 10°C }[/math] and the final temperature of [math]\displaystyle{ T_{\mathrm{final}}= 62°C }[/math]. Therefore we can use the equation
[math]\displaystyle{ \Delta T_{\mathrm{ethyl alcohol}}= T_{\mathrm{final}} - T_{\mathrm{intiall}} }[/math] , to get
[math]\displaystyle{ \Delta T_{\mathrm{ethyl alcohol}}= 62°C-10°C = 52°C }[/math]
And we conclude that the change in temperature or [math]\displaystyle{ \Delta T_{\mathrm{ethyl alcohol}}= 52°C }[/math]
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page