Length and Stiffness of an Interatomic Bond

This topic covers find the length and stiffness of an Interatomic Bond.

The Main Idea

A solid objects is made up of a bunch of tiny balls (atoms) that are held together by springs (chemical bonds). The relaxed legth of the little spring between two atoms (the interatomic bond) is just the distance from the center of one atom to the center of the other atom, d. For our object, the distance is just twice the radius of one of the atoms since the electron cloud of the atom fills in the extra space. If the atoms are in a cubic arrangement that means that the volume of each atom would be d × d × d and would have a cross-sectional area of d × d. Since the interatomic bonds are modeled as springs, they have a stiffness, ks,i, that relates the interatomic force to the stretch of the interatomic bonds. We use s for the microscopic stretch.

We can determine the stiffness of an interatomic bond by considering it as a spring. In order to determine stiffness, we must determine the length of an interatomic bond in a particular material. For different materials, bond lengths will vary slightly depending on the size of the atoms. The length of one interatomic bond is defined as the center-to-center distance between two adjacent atoms. The diameter of an atom is the space-filling model of a solid. To find the radius, we divide the diameter in half. If we can calculate the length of the interatomic bond and the diameter of a single atom, we can use this data to find the stiffness of the interatomic bond, considered as a spring.

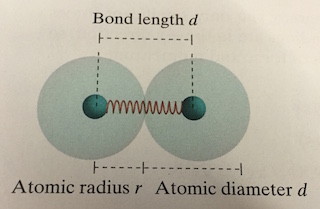
Length of an Interatomic Bond

The length of an interatomic bond is defined as the center-to-center distance between adjacent atoms. This is the same as the diameter of an atom (including the full electron cloud).

We can calculate atomic diameters for crystals of particular elements by using the measured density of the material in kilograms per cubic meter and Avogadro's number (the number of atoms in one mole of the material), 6.02 X 10^23 atoms per 1 mol.

The mass of one atom can be determined using the mass of one mole and dividing it by 6.02 X 10^23 atoms (Avogadro's number)

The Stiffness of an Interatomic Bond

It is difficult to measure the stiffness of an interatomic bond directly, so instead we can analyze data from macroscopic experiments to determine this quantity. We will consider the stiffness of an interatomic bond as a spring.

The equation for stiffness is: |F| = ks,i |s|

Springs in Series

Springs in series refers to when springs are linked end-to-end.

Two identical springs linked end to end stretch twice as much as one spring when the same force is applied. The combined spring therefore is only half as stiff as the individual springs.

Springs in Parallel

Springs in parallel is when springs are linked side-by-side.

We can think of the two springs as a single, wider spring. Two springs side by side are effectively twice as stuff as a single spring.

Cross-Sectional Area

The cross-sectional area of an object is the area of a flat surface made by slicing through the object.

For example, the cross-sectional area of a cylinder is the area of a cicle and the cross-sectional area of a rectangular solid is the area of a rectangle.

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

Middling

Difficult

Connectedness

How is this topic connected to something that you are interested in?
How is it connected to your major?
Is there an interesting industrial application?

References

Matter and Interactions By Ruth W. Chabay, Bruce A. Sherwood - Chapter 4 http://www.webassign.net/question_assets/ncsucalcphysmechl3/lab_10_1/manual.html

Created by Emily Milburn