Transformation of Energy
PLEASE DO NOT EDIT THIS PAGE. COPY THIS TEMPLATE AND PASTE IT INTO A NEW PAGE FOR YOUR TOPIC.
Claimed by Shalim6
This page expands on the ideas presented by the Conservation of Energy and discusses more in detail how energy changes form.
The Main Idea
Energy Transformation is the process in which energy changes from one form, to another. Examples of forms of energy includes: Kinetic, Chemical, Thermal, Gravitational Potential etc. When ever energy changes its form, there is no net loss of energy (Conservation of Energy). Virtually every process we engage in is accompanied by a transformation of energy. Some common everyday examples of energy transformation include, the chemical energy of coal being converted to thermal energy when burned or the conversion of light energy from the sun into electrical energy.
It is important to account for the efficiency of energy transformation. Every energy transformation is accompanied by some change in thermal energy. In other words, it is not possible to convert 100 J of chemical energy to 100 J of kinetic energy, some of that chemical energy will be converted to thermal energy. This is due to friction mainly.

In the figure on the right, there is a candle being burned. When something is burned, the energy stored within the chemical bonds that make of the object are broken and energy is released. In the figure, the chemical of the energy of the candle is being converted into both heat and light. Practically, it would be much more useful if 100% of the chemical energy of the candle was converted to light (the whole point of a candle!). If this were the case, either the candle would burn much brighter, or burn longer, since energy is no longer being wasted as heat. As stated above however, this process is not 100% efficient, and thus, some energy will inevitably will be converted to heat energy.
A Mathematical Model
If we assume that no energy is being converted to work, then we can simply say Einitial = Efinal. Note that E initial and E final don't specify what form energy takes, merely that their intensities are equal in Joules when summed.
A Computational Model
The vpython model on the right depicts a space probe orbiting the earth and moon. The probe is under the influence of the earth and moon's gravity and has it's own initial velocity. The graph on the left shows the kinetic energy of the space probe plotted against the gravitational potential between the space probe and the earth + moon system. The yellow line represents the kinetic energy, the blue line represents the gravitational potential, and the green line represents the these two values added together.
The important part of this demonstration is the conversion of energy. This is a theoretical situation so there is no energy loss as heat. Kinetic energy is being converted to potential energy and vice-versa as you follow you graph. It is important to note that the kinetic energy and potential energy are freely converted between each other freely as the space probe orbits.
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
A candle has 500 J of chemical energy stored in it's wick. After some time, when the entire candle is burned and all the chemical energy is expended,it is found that the candle released 480 J of heat energy. Assuming that the candle only released heat and light energy when it was burned,how much light energy was released by the candle when it was burned?
Since the candle is completely burned, all its chemical energy is completely converted. The problem states that all this energy is converted to either heat or light energy. It is also stated that 480 J of heat energy was released. Therefore, we can write the equation
J chemical energy = J heat energy + J light energy
Thus, 500 = 480 + J light energy
So J light energy = 20 J
Middling
When a person runs a conversion of energy takes place. In this example, use the earth and the person as the system. Write an equation that actually depicts the change in energy of the person and earth system as the person runs down a slope . Assume that the only forms of energy in this equation are gravitational potential, chemical energy, heat, and kinetic energy.
Since humans utilize energy in the form of chemical energy, we start off with a change in chemical energy. When the person accelerates and begins to run, some of the internal chemical energy is converted into kinetic energy. Remember from above that in any change in energy form, some thermal energy is also produced. Notice however, that the person is also running down a slope. This means that the gravitational potential energy between the earth and the person is decreasing. But what is this energy being converted to? The gravitational energy is most likely not forming new chemical bonds in the person's body so it's not chemical energy. It is however possible that this gravitational energy is being converted to kinetic energy, and of course, heat. So we have two sources of kinetic energy, the person converting chemical energy into kinetic energy as well as the earth "pulling the person" downhill increasing his kinetic energy.
We can then write our equation as E chemical + E potential = E kinetic (From chemical) + E kinetic (from gravity) + E heat
Difficult
A water heater is created to heat water for the purpose of turning a turbine. 20 kg of Water at 25 degrees C is heated and forced to evaporate at 100 C per second. Assume the specific heat of water varies little with temperature. This process takes place at 1 atm. This heat energy is being supplied by a stirrer in which 70% of it's kinetic energy is transferred to heat energy per second. Assuming this process is continuous, with 0 accumulation, how much energy must the stirrer transfer to the water per second to achieve this? Assume the process takes place in an adiabatic closed system with a constant volume and pressure.
For this problem we must first determine how much heat is required to evaporate the water, and then heat it to 300 degrees C . The easiest way to do this is using our q = cm delta t equation. First, we heat the water from 25 degrees C to 100 degrees C. This equation becomes --> q = (4.18 kj/kg*C)(20 kg)(100-25 C). We are left with q = 6270 kJ. Now, we need to determine the heat required to convert the water from liquid to a gas. This is also known as the heat of vaporization which is 2257 kj/kg. We can then say q = (2257 kj/kg)(20)Kg we get q = 45,140 kj. Thus, the total heat energy required to raise the water from 25 C to 100 C and then evaporate it is 6270 kj + 45,140 kj = 51,410 kj.
Since the turbine operates at 70% efficiency, we know it must generate more energy than the heat we just found previously. We can simply divide 51,410 by .7 to get 644,871.4 kj. The turbine must generate 644,871.4 kj per second or 644,871 KW.
Connectedness
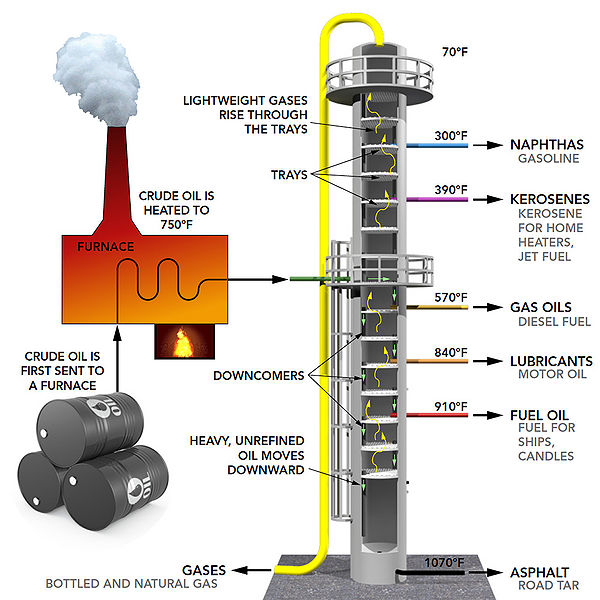
I am currently very interested in oil refinery and as a chemical engineer, I hope to some day work in this sector. Oil is probably one of the most converted energy sources in the world. The whole point of refinery is to extract the maximum amount of usable energy from the chemical bonds of oil. This is accomplished through the use of changing parameters such as pressure, temperature, volume etc. This is directly applicable to energy transformation since the whole point of this process is to use what we know about the properties of oil and make energy efficiency as close to 100% as possible.
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
I used mostly the textbook for this assignment.
Chabay, Ruth W. Matter and Interactions. 3rd ed. Hoboken, N.J.: Wiley ;, 2010. Print.