Werner Heisenberg
created by John Mitchell
Werner Karl Heisenberg was a German Theoretical Physicist who studied quantum mechanics (not to be confused with the drug mastermind from Albuquerque). He is best known for his Uncertainty Principle, which describes the fundamental limit to the accuracy of which the momentum and position of a particle can be measured. He was awarded the Nobel Prize in Physics in 1932 "for the creation of quantum mechanics, the application of which has, inter alia, led to the discovery of the allotropic forms of hydrogen."
Personal Life and Education
Werner Heisenberg was born on Decemeber 5th, 1901 in Würzburg, Germany. He had his primary and secondary education in Munich. He later studied Physics at the University of Munich. Later, in 1922, he went to Göttingen to study physics under Max Born, Franck, and Hilbert. He received his Ph. D at the University of Munich and became Max Born's assistant. In 1924, he worked with Niels Bohr for a year at the University of Copenhagen. In 1927, he became a professor of Theoretical Physics at the University of Leipzig. At the end of the Second World War, He and other German Physicists were taken prisoner by the Allied forces and forced to relocate the United Kingdom. He returned to Germany in 1946 to found the Max Planck Institute for Physics. He died on February 1, 1976 in Munich.
Contributions to Physics
Creation of Quantum Mechanics
Before Heisenberg, the generally accepted model of the atom was that of Niels Bohr, in which the electrons of the atom orbited the nucleus in a circular orbit (a model very similar to the planetary model of the solar system). This model, however, did not account for the predicted properties of atoms and molecules, the nature of light (waves or particles?), or the spectra of emissions emitted by atoms. Heisenberg struggled with the concept of the circular orbits of the electrons as they could not be observed, so he tried to develop his own model of quantum mechanics with what could be observed (the emissions and adsorptions of atoms). Heisenberg's breakthrough, to put it simply, was that in order calculations for particles could not be done using classical arithmetic, but instead with matrices. This version of quantum mechanics was known as "matrix mechanics." This approach to the physics of the atom was revolutionary at the time, because it had a completely different approach to this branch of physics and rejected the classical approach.
The Uncertainty Principle
The Uncertainty Principle is the discovery for which Heisenberg is most well known. As Heisenberg himself put it, the principle states "The more precisely the position [of a particle] is determined, the less precisely the momentum is known in this instant, and vice versa." This is not a statement concerning the inevitable error brought upon by using imprecise equipment: the uncertainty would still exist even with perfect instruments. Mathematically, the Uncertainty Principle is represented with this inequality:
[math]\displaystyle{ \sigma_{x}\sigma_{p} \geq \frac{\hbar}{2} ~~ }[/math]
where σx represents the standard deviation of the position of the particle, where σp represents the standard deviation of the momentum of the particle, and h-bar is Planck's constant divided by 2π. This inequality represents the Principle well, because as the standard deviation (the accuracy with which we are measuring the value) of one of the values decreases (gets more accurate), the standard deviation of the other value must increase (become more inaccurate) in order to be greater than or equal to h-bar divided by 2.
The Principle can also be understood through physical terms. The principle is explained well in this graphic:
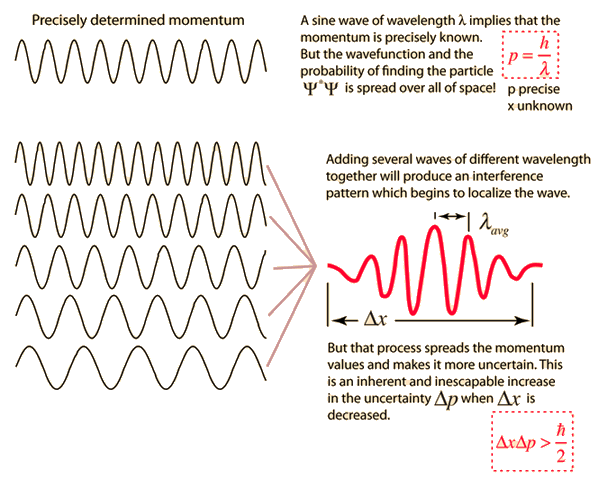
When a particle's precise momentum is known, it can be represented with a perfect sine wave of wavelength λ. While this momentum is known, the exact location of the particle is spread infinitely across the entire x-axis. However (as seen in the picture), adding together momenta with differing wavelengths will cause destructive interference, narrowing the possible area that the particle can be. As more momenta are added, the possible area for the particle's position decreases, which makes us more sure about it's position. However, as more and more momenta are added, the less is known about the particle's momentum. Thus, only one measurement can be precise.
See Also
Further reading
Physics and Philosophy: The Revolution in Modern Science by Werner Heisenberg. Harper Perennial Modern Classics, 1999.
Physics and Beyond: Encounters and Conversations by Werner Heisenberg. Harper Collins Ltd Edition, 1971.
External links
https://en.wikipedia.org/wiki/Werner_Heisenberg
http://www.nobelprize.org/nobel_prizes/physics/laureates/1932/heisenberg-bio.html
References
http://www.nobelprize.org/nobel_prizes/physics/laureates/1932/heisenberg-facts.html