by Julia Logan

Definition

A Mathematical Model

In order to calculate net force, all EXTERNAL forces acting on a system are added together. The mathematical definition is

[math]\displaystyle{ Fnet = F1 + F2 + F3... }[/math]

Additionally,

[math]\displaystyle{ Fnet = ma }[/math]
where m=mass of the object, and a = acceleration of the object.

This is a result of Newton's Second Law of motion. If there is a nonzero net force acting on an object, that object is accelerating (not traveling at a constant velocity). Interestingly, there is zero net force acting on an object if its velocity is constant. This seems counter-intuitive (surely something is causing the object to move!) but makes sense in the context of Newton's Second Law. The forces are balanced (sum to zero) if there is no acceleration, despite any movement that may be happening.

A Computational Model

Net force is an essential component of the Momentum Principle! We can use the Momentum Principle in vpython to update the position of a moving object. But first, we have to find net force.

Tracing the path of a ball/spring model in vpython using net force and the momentum principle.

  #1 Fspring = -k*s
  #2 Fgravmag = mball * g
  #3 Fgrav = Fgravmag * vector(0,-1,0)
  #4 Fnet = Fspring+Fgrav
  #5 pball = pball + Fnet * deltat
  #6 vball = pball / mball
  #7 ball.pos=ball.pos+vball*deltat

Here, the spring force and the gravitational force are found using formulas (lines 1-3). Then, they are added together to get the net force on the object (in this case a ball, line 4). The net force is then used in the update form of the momentum principle (line 5). In line 6 the velocity is updated, and line 7 the position is updated. Without net force calculations, tracing an object's path would be impossible.

Simple Example

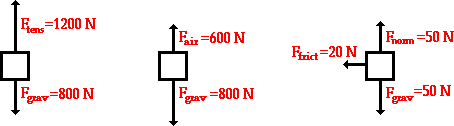
When calculating net force, it is most useful to construct a free body diagram. A free body diagram is a physical representation of the external forces applied to a system. Often, arrows are used to represent forces. In this example, forces are displayed acting on a box.

The first two boxes' net force can be easily calculated by adding the two forces acting on them, respectively. With down being in the negative y direction, for the first box we have:

[math]\displaystyle{ Fnet = (0, 1200, 0) N + (0, -800, 0) N }[/math]
[math]\displaystyle{ Fnet = (0, 400, 0) N }[/math]

And the second box:

[math]\displaystyle{ Fnet = (0, 600, 0) N + (0, -800, 0) N }[/math]
[math]\displaystyle{ Fnet = (0, -200, 0) N }[/math]

The third box has both x-component forces and y-component forces. It is important to separate these in solving for the net force.
y-components:
[math]\displaystyle{ Fnet,y = (0, 50, 0) N + (0, -50, 0) N }[/math]
[math]\displaystyle{ Fnet,y = (0, 0, 0) N }[/math]
x-components:
[math]\displaystyle{ Fnet,x = (-20, 0, 0) N + (0, 0, 0) N }[/math]
Put them together:
[math]\displaystyle{ Fnet = (-20, 0, 0) N }[/math]

Connectedness

Net force is one of the building blocks of Intro Physics, and I would assume all of physics. It's really important for all motion-related topics, specifically curving motion. A net force due to the gravitational pull of the Sun in the perpendicular direction is how the Earth revolves around the Sun -- why we have days and nights and years! Pretty cool.

History

Initially it was believed that force was required to maintain a constant velocity, but this was later cleared up by Sir Isaac Newton's laws of motion and Einstein's theory of relativity in the early 20th century.

References

Cardenas, Richard. "What is Net Force? - Definition, Magnitude & Equations." Web. 30 Nov 2015. http://study.com/academy/lesson/what-is-net-force-definition-magnitude-equations.html

"Net Force." Wikipedia: The Free Encyclopedia. Wikimedia Foundation, Inc. Web. 30 Nov 2015. https://en.wikipedia.org/wiki/Net_force

The Physics Classroom. "Determining the Net Force." Web. 30 Nov 2015. http://www.physicsclassroom.com/class/newtlaws/Lesson-2/Determining-the-Net-Force

Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. Modern Mechanics. Hoboken, NJ: Wiley, 2011. Print.

Net Force

Contents