Moment of Inertia for a cylinder
This page discusses the moment of inertia specifically in the case of a cylinder or rod.
Written by Jack Corelli
A Brief Overview
See The Moments of Inertia for a more general explanation of moments of inertia.
The moment of inertia of an object relates the mass of the object, the distance between the center of mass and the shape of rotation. In a ring, or uniform loop, the center of mass is exactly at the center of the ring, and the moment of inertia can be found by approximating the exterior ring as a single line, akin to a circle.
Governing Equations
In its simplest form, the moment of inertia can be found for a simple, constant density and shape rod by the equation:
[math]\displaystyle{ I = \frac{1}{2}*M*R^2 }[/math] Where I is the moment of inertia, M is the mass of the object being rotated and R is the radius of the rod. This describes the moment of inertia calculated when a rod is spun about its center axis.
As can be seen here:
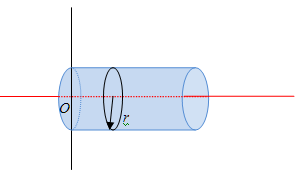
If the axis of rotation is no longer the center of the cylinder or rod, the equations for moment of inertia change distinctly. At the center of a rod, with the axis of rotation perpendicular to the length:
[math]\displaystyle{ I = \frac{1}{4}*M*R^2 + \frac{1}{12}*M*L^2 }[/math]
As can be seen here:
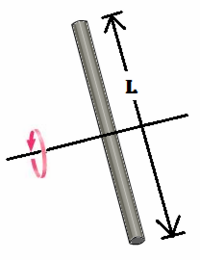
If the axis of rotation has the same direction as the second equation, that is perpendicular to the length, but is at the end of the rod, just touching one of the circular caps, then the equation would be: [math]\displaystyle{ I = \frac{1}{4}*M*R^2 + \frac{1}{3}*M*L^2 }[/math]
As can be seen here:
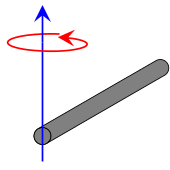
Examples
Connectedness
- How is this topic connected to something that you are interested in?
Moments of Inertia are very important in industrial processes, especially for engines. Think of a wind turbine. That is essentially the third equation above, and if an engineer wanted to figure out how much force would be needed to slow the blade, that is one of the components in that equation.
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
You can find more information in the text book about moments of inertia for different sized objects.
http://hyperphysics.phy-astr.gsu.edu/hbase/mi.html