Standing waves
Claimed by Anviksha Busa
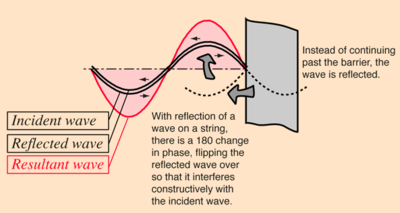
The modes of vibration associated with resonance in extended objects like strings and air columns have characteristic patterns called standing waves. These standing wave modes arise from the combination of reflection and interference such that the reflected waves interfere constructively with the incident waves. An important part of the condition for this constructive interference for stretched strings is the fact that the waves change phase upon reflection from a fixed end. Under these conditions, the medium appears to vibrate in segments or regions and the fact that these vibrations are made up of traveling waves is not apparent - hence the term "standing wave".
The behavior of the waves at the points of minimum and maximum vibrations (nodes and antinodes) contributes to the constructive interference which forms the resonant standing waves. The illustration above involves the transverse waves on a string, but standing waves also occur with the longitudinal waves in an air column. Standing waves in air columns also form nodes and antinodes, but the phase changes involved must be separately examined for the case of air columns.
Characteristics of a Standing Wave
State, in your own words, the main idea for this topic Electric Field of Capacitor
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
Nodes and Antinodes
Standing waves on a string are a result of traveling waves interfering both destructively and constructively. The nodes (places of zero amplitude) are due to destructive interference, and the antinodes (places of maximum amplitude) are due to constructive interference. When a standing wave appears, the nodes and antinodes are fixed in place. When the conditions of the tension in the string, the linear density and the frequency of oscillations are just right, standing waves appear.
-
Standing wave in stationary medium. The red dots represent the wave nodes.
-
A standing wave (black) depicted as the sum of two propagating waves traveling in opposite directions (red and blue).
The pattern above is not the only pattern of vibration for a guitar string. There are a variety of patterns by which the guitar string could naturally vibrate. Each pattern is associated with one of the natural frequencies of the guitar strings. Three other patterns are shown in the diagrams at the right. Each standing wave pattern is referred to as a harmonic of the instrument (in this case, the guitar string). The three diagrams at the right represent the standing wave patterns for the first, second, and third harmonics of a guitar string. (Harmonics will be discussed in more detail in the next section of this lesson.)
There are a variety of other low energy vibrational patterns that could be established in the string. For guitar strings, each pattern is characterized by some basic traits:
There is an alternating pattern of nodes and antinodes. There are either a half-number or a whole number of waves within the pattern established on the string. Nodal positions (points of no displacement) are established at the ends of the string where the string is clamped down in a fixed position. One pattern is related to the next pattern by the addition (or subtraction) of one or more nodes (and antinodes).
Standing Wave Patterns
====First Harmonic====
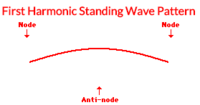
The simplest standing wave pattern has points of no displacement (nodes) at the two ends and one point of maximum displacement (antinode) in the middle. This is the first harmonic. It is the simplest wave pattern produced and is obtained when the teacher introduced vibrations into the end of the medium at low frequencies.
====Second Harmonic====
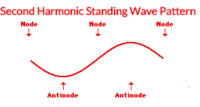
Other wave patterns can be observed when it is vibrated at greater frequencies. For instance, if the teacher vibrates the end with twice the frequency as that associated with the first harmonic, then a second standing wave pattern can be achieved. This standing wave pattern is characterized by nodes on the two ends and an additional node in the exact center. As in all standing wave patterns, every node is separated by an antinode. This pattern with three nodes and two antinodes is referred to as the second harmonic.
====Third Harmonic====
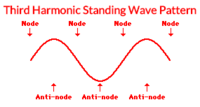
If the frequency is increased even more, then the third harmonic wave pattern can be produced. The standing wave pattern for the third harmonic has an additional node and antinode between its ends.
====Other Harmonics====

As one studies harmonics and their standing wave patterns, it becomes evident that there is a predictability about them. Not surprisingly, this predictability expresses itself in a series of mathematical relationships that relate the wavelength of the wave pattern to the length of the medium. Additionally, the frequency of each harmonic is mathematically related to the frequency of the first harmonic. Each consecutive harmonic is characterized by having one additional node and antinode compared to the previous one
Mathematical model: Standing waves with different ends
Be sure to show all steps in your solution and include diagrams whenever possible
2 fixed ends
What are the mathematical equations that allow us to model this topic. For example [math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{system} = \vec{F}_{net} }[/math] where p is the momentum of the system and F is the net force from the surroundings.
A wave has both a frequency and a wavelength that are related by the following equation:
[math]\displaystyle{ {λf = v} }[/math]
Where λ is the wavelength, f the frequency, and v the velocity of the wave on the string. The wavelengths of the standing waves are fixed by the length of the string. As both ends are fixed, there must be a node at each end of the string. As the standing waves on the string are sinusoidal, the allowed number of waves on the string will be an integral number of half wavelengths, or:
nλ/2 = L
[math]\displaystyle{ {\frac{nλ}{2}} = L} }[/math]
where n is a positive integer, λ the wavelength, and L the length of the string.
1 fixed end
Application
Standing waves are used and seen in multiple real life examples. It is a major contributor in quantum mechanics. It can also be found in the following:
-In string instruments, a plucked or bowed string makes the note is does because only certain frequencies of stationary (or "standing") waves are able to form on that string under those conditions (e.g., a finger holding down the string at a certain position). Any vibrations that aren't at the right frequencies to make standing waves quickly cancel themselves out, and so it's the standing wave frequencies that we actually hear.
-Similarly, for woodwind instruments, we get the notes we get because of what standing waves are able to form within the tube of air inside the instrument. (Strings and woodwinds sound different from one another because they allow different combinations of overtones (higher-frequency standing waves) to form.)
-Waves on the beach
-When you tune in a radio station, you are making the antenna circuit resonate with a particular carrier wave. The radio wave induces a standing wave of alternating current in the antenna circuit.
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
http://web.stanford.edu/dept/astro/dorris/StandingWaves.pdf https://en.wikipedia.org/wiki/Standing_wave http://hyperphysics.phy-astr.gsu.edu/hbase/waves/standw.html#c4 http://hyperphysics.phy-astr.gsu.edu/hbase/waves/funhar.html#c3