Free Body Diagram

Claimed by Whitney Graham

Main Idea

What are Free Body Diagrams?

A free body diagram, or force diagram, is a rough sketch that shows all the forces acting on a system. There are various forces that can be acting on the object, such as applied force, frictional force, normal force, and gravitational force. All forces in a free body diagram are due to the system's interactions with its surroundings. Especially when problems become complicated and involve different forces acting on multiple objects, free body diagrams can be extremely effective in making a problem simpler to handle.

Relation to Newton's Second Law

Free body diagrams are usually used in collaboration with Newton's Second Law, F=mass*acceleration, as both are typically used in the process of solving for force. Newton's Second Law is the sum of the forces. The sum of the forces is equal to zero when the object is not accelerating or is moving at constant velocity.

How To Draw a Free Body Diagram

(1) Identify the system

(2) List and identify all objects in the system's surroundings that interact with the system

Although we usually think of these interactions in terms of force names, it's best to get in the habit of identifying the force AND the object that specifically causes that force. For example, the force of gravity on a block could be caused by the earth. Or a normal force could be caused by a second block and another normal force could be caused by the table. Identifying forces by the specific objects that cause them helps us not forget forces.

Types of Forces to Consider for Free Body Diagrams:

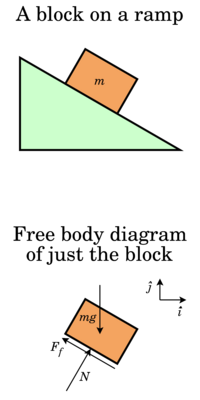
Disclaimer: Not all of these forces will be present in every situation. These are not all possible choices of forces, just the most common in a Physics 1 course.

Applied Force: Force applied to the system by a person or other object.
Force of Friction: Force that a surface applies on the system that is moving (or trying to move) on that surface.
- Formula: f=μN
- f = Frictional Force
- N = Normal Force
- μ = Coefficient of Friction
Force of Gravity: Force that, on Earth, will act downward toward the center of the Earth.
- Formula: Force of gravity = mg
- m = mass
- g = 9.8 m/s^2 (on earth) OR -(GMm)/r^2
Normal force: Force that is present when the system is on another object or surface, and the object or surface is exerting a force on the system as support.
Spring force: Force that is exerted by a spring onto any system that is attached to it.
- Formula: Spring force=-kx
- k = spring constant
- x = displacement from the spring's relaxed position
Force of tension: Force that exists when a rope, string, wire, etc. is pulling on the system.

(3) Draw a diagram with the system at the center

Can use a dot to represent the system, OR
Can draw the details of the system (Draw a block, car, etc.)

(4) Draw all the forces acting on the system (represented as arrows).

Arrow length should represent the approximate magnitude of that force relative to other forces

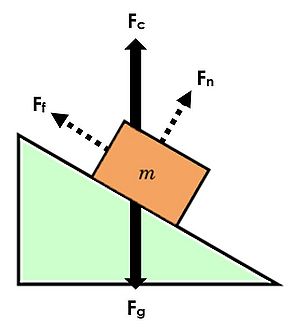
(5) Label all forces with a symbol representing the name of the force and identify them by the object causing the force

Examples of force symbols:

Fg (force of gravity)
Ff (force of friction)
Ft (force of tension)
Fn (normal force)
Fc (contact force)

Examples of objects causing the force:

Earth
Ramp
Block
Rope
Moon
Spring

(6) Break forces into their components as needed.

If a force is acting diagonal to the system, create a dashed line parallel and perpendicular to the system and label it as the x and y components of that force. Use sine(θ) or cosine(θ) as needed.

General Tips:

If an object has constant speed, it means the object has no acceleration. Since net force is the rate of change of acceleration, net force in that direction would then be zero. This means that there are either no forces currently acting on the object, or there are equal, opposite forces acting on the object in that direction. To represent this in a free body diagram, draw forces as arrows pointing in opposite directions with equal lengths.
Don't be confused by contact forces. Most of the time, contact force is an umbrella term that includes other types of forces. If you had a block on a ramp, you could draw the contact force as being diagonal to the ramp. Or, if you wanted to break it into its components which are easier to consider, you would draw the Normal force caused by the ramp pushing up as a perpendicular arrow, and the force of Friction caused by the ramp as a parallel arrow (see image to the upper right).

Examples

Simple

Example 1 (IN-DEPTH, following the steps outlined above).

Identify the system: block
List all objects interacting with the system:

Ramp
Earth

Draw a diagram of the system: We drew a block to represent the system
Draw all forces acting on the system: Because the block is stationary, we know it is not accelerating in the x nor y directions, so net force in the x and y directions is zero. Thus, the arrows in the y direction have equal length and no arrows are in the x direction.
Label all forces with a force symbol and identify the object causing the force

Contact force, Fc, caused by the ramp
Force of gravity, Fg, caused by the earth

Break forces into components: We can break up the contact force into normal force and force of friction.

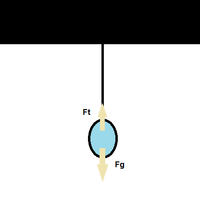
Example 1: A person rides in an elevator moving at constant velocity. Create a free body diagram to represent this situation.

Example 1 Solution-In this example, the only forces acting on the system are the force of gravity and the normal force

Middling

Example 2: A ball is hanging on a string of negligible mass from the ceiling. Create a free body diagram to model this situation.

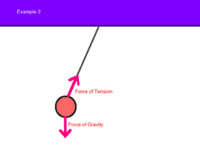
Example 2 Solution-In this example, the only forces acting on the system are the force of gravity and the force of tension

Note: For this example, when solving for forces, the force of tension must be split into horizontal and vertical components and solved.

Difficult

Example 3: A stationary box lies on an incline. Create a free body diagram to model this situation.

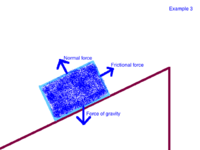
Example 3 Solution-In this example, the forces acting on this system are the force of gravity, the force of friction, and the normal force.

Note: Friction is necessary to keep the box stationary. When solving for the normal force and for frictional force, both the x and y component must be considered.

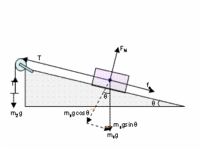
This, found from http://demos.smu.ca/index.php/demos/mechanics/141-free-body-diagram, is a more complicated problem to show that free body diagrams prove extremely helpful when sorting out problems with multiple different objects being acting upon.

Diagrams with solution are on the left and right.

Connectedness

While free body diagrams do not necessarily correlate with my life, they do have an application in the real world. For example, companies designing things such as billboards and even things such as houses, free body diagrams can be used to solve for how much force the structure must be supporting before construction begins.

History

References

Matter and Interactions: Modern Mechanics. Volume One. 4th Edition.

http://demos.smu.ca/index.php/demos/mechanics/141-free-body-diagram

http://hyperphysics.phy-astr.gsu.edu/hbase/freeb.html

https://www.wisc-online.com/learn/natural-science/physics/tp1502/construction-of-free-body-diagrams

http://www.physicsclassroom.com/Class/newtlaws