Compression or Normal Force

Claimed by Hemanth Koralla

Compression of Normal Force

The compression or also commonly known as the normal force, [math]\displaystyle{ F_n\ }[/math], is a simple fundamental concept that must be understood before attempting any contact force problem. First, it is important to understand that the normal force is NOT a kind of fundamental force such as the electric or gravitational force. It is just a force used to describe the interaction between atoms. As hinted by the name, this force simply points in the perpendicular or "normal" direction to the surface(s) that it is in contact with. The magnitude of this normal force is often equal to the weight of the object, however, objects can move along surfaces with various angles. This results in the normal force being present in both the direction parallel and perpendicular to the surface.

Understanding information about the normal force on an object can also help . The approximate force of friction is the static friction coefficient multiplied by this normal force.

Equations

The formula for calculating the normal force is dependent on the positioning of the system, however, the most commonly used formula for normal force is represented below:

[math]\displaystyle{ F_n = mg }[/math]

[math]\displaystyle{ F_n }[/math] is the normal force of the system

[math]\displaystyle{ m }[/math] is the mass of the system

[math]\displaystyle{ g }[/math] is a constant value for the force due to gravity and is equivalent to 9.8 [math]\displaystyle{ m/s^2 }[/math]

The formula for calculating the force of friction using this normal force when an object is on an inclined plane is:

[math]\displaystyle{ F_f (static) = \muF_n }[/math]

[math]\displaystyle{ = \mumg \cos(\theta)) }[/math]

[math]\displaystyle{ \mu }[/math] = coefficient of static or kinetic friction

[math]\displaystyle{ m }[/math] is the mass of the system

[math]\displaystyle{ g }[/math] is a constant value for the force due to gravity and is equivalent to 9.8 [math]\displaystyle{ m/s^2 }[/math]

Examples

The examples below represent different situations in which the net force changes due to the placement of the system.

Simple

On the image to the left (Example 1), there is a 7 kilogram block resting on top a flat table. Find the normal force, [math]\displaystyle{ F_n\ }[/math], that is being exerted on the block. The force of gravity is 9.8 N/kg.

Answer

Fn = mgcos(theta)
In this example, theta will be 90 since the normal force is perpendicular to the surface that it is resting on, thus 90 degrees. 
Now we can plug into our formula: 
m = 7kg
g = 9.8 N/kg
[math]\displaystyle{  F_n = mg }[/math]
Fn = (7 kg)(9.8 N/kg)
 = 68.6 N

Middling

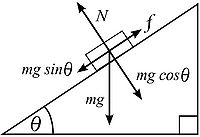
A 14 kg block is lying stationary on a plane that is inclined 48 degrees. Find the normal force perpendicular to the block on the incline using the accompanying image to the right. The force of gravity is [math]\displaystyle{ 9.8 m/S^2 }[/math].

Answer

Because this problem asks for the normal force on an inclined plane, it is important to break up the normal force into components:

Given:
m = 14 kg
g = 9.8 N/kg
theta = 48

By analyzing the image, it is seen that the cosine trig identity correlates to the direction in which the normal force is perpendicular to the surface. Multiplying the mass of the block and force of gravity by the cosine of the stated angle, the perpendicular normal force will be found.

[math]\displaystyle{ F_n = mgcos(\theta) }[/math] [math]\displaystyle{ F_n = (14 kg)(9.8 m/s^2)cos(48) }[/math] [math]\displaystyle{ = 91.805 N }[/math]

Connectedness

This force is very crucial to understand because it explains the fundamental reason for why gravity doesn't keep pulling us down and explains this not-so-apparent force that is acting on an object. It helps explain why objects do not keep falling into the Earth. The application of the normal force can be seen in many industrial situations. It must be taken into account when drawing free body diagrams, such as for construction and architectural purposes.

History

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Sir Isaac Newton

The normal force a direct application of Newton's Third Law of Motion. Sir Isaac Newton was a famous scientist from England who roamed the Earth from 1643 to 1727. His work in math and physics set the stage for many of the principles and theories that we have today. His main work, the Philosophiae Naturalis Principia Mathematic, discussed many of his theories about physics and stated his three laws of motion. The application of Newton's three laws of motion extend to today's uses due to the important of understanding how much