Lorentz Force

Claimed by Firas Sheikh- 1 November 2015 (EST)

Improved by Anna Marie Whitacre (SPRING 2016)

The Main Idea

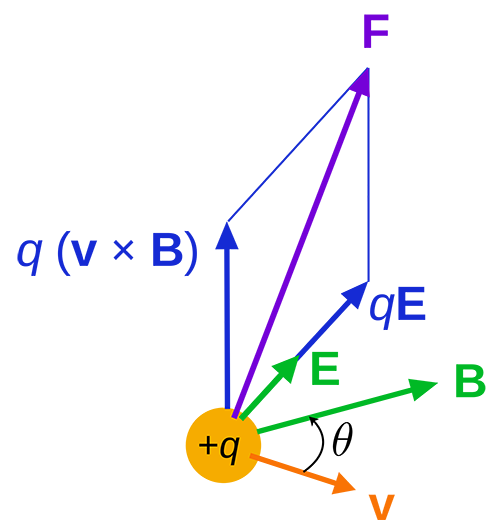
The Electric and Magnetic Forces can be combined into a single force called the "Lorentz Force." This combination of the two forces is useful in applications where a magnetic field and electric field act on a specific particle or series of particles.

A Mathematical Model

[math]\displaystyle{ \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B} }[/math] where [math]\displaystyle{ q\vec{E} }[/math] is the electric force and [math]\displaystyle{ q\vec{v} ⨯ \vec{B} }[/math] is the magnetic force.

A Computational Model

Examples

Simple

If the Electric Force points in the +x direction and the Magnetic Force points in the –x direction, what direction the Lorentz force point in?

Solution: The Lorentz Force is 0 N.

Middling

The electric force on a certain particle is <500,-200,300> N and the magnetic force is <-200,700,400> N. Find the Lorentz force.

Solution:

Lorentz Force = Electric Force + Magnetic Force

Lorentz Force = <500,-200,300> + <-200,700,400> = <300,500,700> N

Difficult

The speed of the proton is 5e3 m/s. The magnitude of the Electric Field on the proton is 8e-6 N/C and the magnitude of the magnetic field at that same proton is 4e-9 T. Find the Lorentz Force on this proton.

Solution:

Electric Force = qE = (1.6e-19)*(8e-6) = 1.28e-24 N

Magnetic Force = q*B*v = (1.6e-19)*(4e-9)*(5e3) = 3.2e-24 N

Lorentz Force = Force Electric + Force Magnetic = 4.48e-24 N

Connectedness

Hovering spacecraft

1. I am interested in hovering spacecrafts and the Lorentz force can be useful for this topic. Assuming that the Earth's magnetic field is a dipole that rotates with the Earth, a dynamical model that characterizes the relative motion of Lorentz spacecraft is derived to analyze the required open-loop control acceleration for hovering. What must be understood first is the hovering configurations that could achieve hovering without a propellor and the corresponding required specific charge of a Lorentz spacecraft.

Simplified sketch of the LFF

2. As an aerospace engineering major, I can investigate the feasibility of using the induced Lorentz force as an auxiliary means of propulsion for spacecraft hovering. To achieve hovering, a spacecraft thrusts continuously to induce an equilibrium state at a desired position. Due to the constraints on the quantity of propellant onboard, long-time hovering around low-Earth orbits (LEO) is hardly achievable using traditional chemical propulsion. The Lorentz force, acting on an electrostatically charged spacecraft as it moves through a planetary magnetic field, provides a new method for orbital maneuvers without propellant.

3. In metallurgic industry the in-situ measurement of the flow rate of metal melts is still an unsolved problem. Due to the chemical aggressiveness of high-temperature melts, classical measurement techniques such as fly-wheel, Pitot tube, and hotwire probes cannot be used as these methods require mechanical contact with the melt. This is where the calibration of a non-contact electromagnetic flow rate measurement device called Lorentz force flow meter (LFF) comes in handy. To use this Lorentz force flow meter in industrial applications with a determined accuracy, a proper calibration of the flow meter has to be performed beforehand. To this aim, a two-step calibration method consisting of a dry and a wet technique must be performed.

History

Early attempts to quantitatively describe the electromagnetic force were made in the mid-18th century. It was proposed that the force on magnetic poles, by Johann Tobias Mayer and others in 1760, and electrically charged objects, by Henry Cavendish in 1762, obeyed an inverse-square law. However, in both cases the experimental proof was neither complete nor conclusive. It was not until 1784 when Charles de Coulomb, using a torsion balance, was able to definitively show through experiment that this was true. Soon after the discovery in 1820 by Hans Christian Ørsted that a magnetic needle is acted on by a voltaic current, Andre Marie Ampere that same year was able to devise through experimentation the formula for the angular dependence of the force between two current elements. In all these descriptions, the force was always given in terms of the properties of the objects involved and the distances between them rather than in terms of electric and magnetic fields.

The modern concept of electric and magnetic fields first arose in the theories of Michael Faraday, particularly his idea of lines of force, later to be given full mathematical description by William Thomson (Lord Kelvin) and James Maxwell. From a modern perspective it is possible to identify in Maxwell's 1865 formulation of his field equations a form of the Lorentz force equation in relation to electric currents, however, in the time of Maxwell it was not evident how his equations related to the forces on moving charged objects. J. J. Thomson was the first to attempt to derive from Maxwell's field equations the electromagnetic forces on a moving charged object in terms of the object's properties and external fields. Interested in determining the electromagnetic behavior of the charged particles in cathode rays, Thomson published a paper in 1881 wherein he gave the force on the particles due to an external magnetic field as F = (q/2)*v X B.

See also

The Hall Effect explores this concept more in depth because it deals with the Electric Force and Magnetic Force being equal. Usually, these problems require you to set them equal to each other and solve for B,v, or E.

Further reading

• http://hyperphysics.phy-astr.gsu.edu/HBASE/hframe.html
• http://www.ittc.ku.edu/~jstiles/220/handouts/section%203_6%20The%20Lorentz%20Force%20Law%20package.pdf

External links

• http://jnaudin.free.fr/lifters/lorentz/
• https://nationalmaglab.org/education/magnet-academy/watch-play/interactive/lorentz-force

References

• Feynman, Richard Phillips; Leighton, Robert B.; Sands, Matthew L. (2006). The Feynman lectures on physics (3 vol.). Pearson / Addison-Wesley. ISBN 0-8053-9047-2.: volume 2.
• Jackson, John David (1999). Classical electrodynamics (3rd ed.). New York, [NY.]: Wiley. ISBN 0-471-30932-X.
• Serway, Raymond A.; Jewett, John W., Jr. (2004). Physics for scientists and engineers, with modern physics. Belmont, [CA.]: Thomson Brooks/Cole. ISBN 0-534-40846-X.