RC Circuit
CLAIMED BY MARK RUSSELL SPRING 2016

The Main Idea
An RC circuit is a circuit that contains a battery with a known emf, a resistor (R), and a capacitor (C). An RC circuit can be in either series or parallel. The figure in the top right of the page shows an RC circuit. The capacitor stores electric charge (Q)
RC Circuits use a DC (direct current) voltage source and the capacitor is uncharged at its initial state. In the figure below, you see an RC circuit with a switch. When the switch is closed, the capacitor will begin to charge as the current can now flow throughout the circuit. To discharge the capacitor, you simply disconnect the switch.

Remember that potential difference across the capacitor is delta [math]\displaystyle{ {V} = {Q}/{C} }[/math], where Q is charge on the plate and C is the capacitance. When the switch is closed, voltage on the capacitor rises rapidly at first, due to the high current at [math]\displaystyle{ {time} = {0} }[/math]. The voltage opposes the battery, increasing from zero to the max emf when the capacitor is fully charged. The current decreases from its initial value of [math]\displaystyle{ {I}_{0} = {emf}/{R} }[/math] to zero as the voltage on the capacitor reaches the same value as the emf. The current is initially at its max at time [math]\displaystyle{ {t} = {0} }[/math]. Once the potential difference across the plates of the capacitor equals the battery's voltage supply, current will stop flowing through the circuit. This is known as the steady state of an RC circuit; it is reached when time goes to infinity.
Using derived calculus, the equation for voltage versus time when the capacitor is charged through resistor R is [math]\displaystyle{ {V} = {emf(1-e^{\frac{-t}{RC}})} }[/math]. [math]\displaystyle{ {V} }[/math] is defined as the voltage across the capacitor. [math]\displaystyle{ {emf} }[/math] is equal to the emf of the DC voltage source. The units of [math]\displaystyle{ {RC} }[/math] are in seconds. [math]\displaystyle{ {τ} = {RC} }[/math]. [math]\displaystyle{ {τ} }[/math] is the constant of time in the RC circuit.
The smaller the resistance, the faster a capacitor will be charged. It takes longer to charge than to discharge. This is because a larger current flows through a smaller resistance ([math]\displaystyle{ {I} = {V/R} }[/math]). Also the smaller the capacitor (C), the less time it will need to charge. [math]\displaystyle{ {τ} = {RC} }[/math] explains both of these.
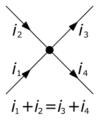
Kirchoff's Node Rule is important to RC Circuits because finding the current flow in the different states of an RC Circuit often relies on nodes when the capacitor is in a parallel circuit.
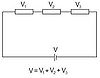
Kirchhoff’s loop rule explains that the sum of changes in potential around any closed loop must be zero.
A Mathematical Model
These three equations are helpful in solving and understanding RC circuit problems
[math]\displaystyle{ {ΔV}_{round trip} = {0} }[/math]
[math]\displaystyle{ {ΔV} = {I}{R} }[/math]
[math]\displaystyle{ {Q} = {C}{V} }[/math]
In a loop of a circuit, the change of potential difference has to be zero. The energy equation for the RC Circuit in the figure at the top of the page is:
[math]\displaystyle{ {ΔV}_{round trip} = emf-RI-Q/C = 0 }[/math]
At the final state of the circuit after the current has dropped to zero and the capacitor is fully charged, [math]\displaystyle{ {RI} = {0} }[/math]. The new equation for the final state is:
[math]\displaystyle{ {V}_{round trip} = emf-Q/C = 0 }[/math]
[math]\displaystyle{ {Q} = emf*C }[/math]
To find the equation for voltage versus time when charging a capacitor through a resistor, you start with rearranging the energy equation and solving for I:
[math]\displaystyle{ {I} = {\frac{dQ}{dt}}={\frac{emf-Q/C}{R}} }[/math]
You know that [math]\displaystyle{ {I} = {\frac{dQ}{dt}} }[/math] due to the rate at which charge builds up the positive capactior plate.
[math]\displaystyle{ {I} = {\frac{dQ}{dt}}={\frac{emf-Q/C}{R}} }[/math]
If you exponentiate both sides, the following equation is achieved.
[math]\displaystyle{ {\frac{IR}{emf}} = {e^{\frac{-t}{RC}}} }[/math]
[math]\displaystyle{ {I} = {\frac{emf}{R}e^{\frac{-t}{RC}}={\frac{dQ}{dt}}} }[/math]
[math]\displaystyle{ {dQ} = \int_0^t{\frac{emf}{R}e^{\frac{-t}{RC}}\,\mathrm{d}t} }[/math]
[math]\displaystyle{ {Q} = {C(emf)(1-e^{\frac{-t}{RC}})} }[/math].
Since [math]\displaystyle{ {V} = {Q/C} }[/math], thus
[math]\displaystyle{ {V} = {emf(1-e^{\frac{-t}{RC}})} }[/math].
This is the formula for the change in voltage of a series RC circuit with respect to time.
The RC time constant formula is:
[math]\displaystyle{ {τ} = {RC} }[/math]
Examples
Simple
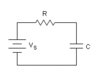
In the steady state what is the potential difference across the plates of the capacitor? The circuit has a resistor, R, capacitor, C, and battery, Vs.
Solution: The key concept in this problem is that in the steady state time is approaching infinity. In an RC circuit as time approaches infinity, the current is 0 because the potential difference across the capacitor equals that of the battery. Therefore, the potential difference across the plates of the capacitor equals Vs.
Difficult
The circuit below has been in position a for a long time. At time t = 0 the switch is thrown to position b. DATA: Vb = 12 V, C = 10 mF, R = 20 W
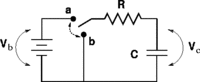
a.) What is the current through the resistor just BEFORE the switch is thrown?
The circuit is in a steady state so I = 0
b.) What is the current through the resistor just AFTER the switch is thrown?
Solution: I = V/R I = 0.6 amps since the capacitor has a potential difference and is creating the current.
c.) What is the charge across the capacitor just BEFORE the switch is thrown?
Solution: Q = CV Q = 120 mC
d.) What is the charge on the capacitor just AFTER the switch is thrown?
Solution: Charge does not change instantaneously Q = 120mC
Connectedness
- How is this topic connected to something that you are interested in?
- RC Circuits can be used in musical instruments such as guitars and amplifiers. I play the guitar so it is cool to see how the guitar actually works.
- How is it connected to your major?
- Mechanical Engineering requires the use of many electronics and learning how various circuits work is necessary for creating new parts and machines.
- Is there an interesting industrial application?
RC circuits can be used in many industrial areas to allow certain frequencies to pass through a circuit.
See also
Further reading
External links
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/rcimp.html
References
http://www.electronics-tutorials.ws/rc/rc_1.html
https://www.pa.msu.edu/courses/1997spring/PHY232/lectures/kirchoff/examples.html