Resistivity

Claimed by Brian Duffy -- Fall 2016

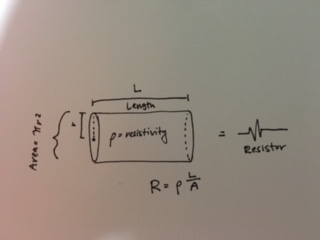
Resistivity is the measure of a specific materials ability to impede the flow of an electric current. The SI unit of resistivity is measured in Ohms per meter, ([math]\displaystyle{ ({Ohm}⋅{Meter}) }[/math] or [math]\displaystyle{ ({Ω}⋅{m}) }[/math]) and is used to determine the resistance of a given conductor. Resistivity of an object is almost entirely dependent on two specific factors: temperature and material. Resistivity is totally dependent of the shape or size of whatever material, which is different from overall resistance (which depends on resistivity, length and cross-sectional area of the object).

The Main Idea

Resistivity is essentially a constant that describes the resistability of a specific material with respect to the current that passes through it. Some materials will more readily allow the flow of current in comparison to others. For instance, copper has half the resistivity as that of aluminum. Thus, most wires are made out of copper instead of aluminum -- as aluminum impedes the flow of electrical current. Materials like glass, which are poor conductors usually have very high resistivity, and metals which conduct electricity well have much lower resistivity.

A Mathematical Model

Resistance is often calculated from resistivity using the following equation [math]\displaystyle{ R = \frac{\rho L}{A} }[/math] where R is the resistance [math]\displaystyle{ \rho }[/math] is the resistivity, L is the length, and A is the cross-sectional area. While the area of the wire or object may be variable, as well as the length, resistivity remains constant because the material remains constant.

In a circuit the Electrical Resistance is then used to calculate the current in a circuit using Ohm's Law and the following equation [math]\displaystyle{ I = \frac{|\Delta V|}{R} }[/math] where V is the voltage, I is the current, and R is the resistance. In this equations voltage and resistance are independent variables, whereas the Current is the dependent variable. This law, while useful, only works for ohmic resistors.

The definition provided above is specific to ohmic resistors, as stated. These resistors have a uniform cross-section, where current flows uniformly through them. Instead, a more general definition starts with the idea that an electric field inside a specific material is responsible for the electric current flowing within it. Because most of the resistors we will deal with are uniform, a simple ratio of field to current can be used in regards to resistivity. Thus, the electrical resistivity, or "p" can be defined as the ratio of the electric field to the density of the current it creates:

[math]\displaystyle{ \rho=\frac{E}{J}, \,\! }[/math]

where "ρ" is the resistivity (ohm⋅meter), "E" is the magnitude of the electric field (volts per meter), and J is the magnitude of the current density (amperes per square meter).

Note, remember above where objects with higher resistance are worse conductors and vice versa; this can be seen when E and J are inside the conductor. Conductivity is the inverse of resistivity:

[math]\displaystyle{ \sigma=\frac{1}{\rho} = \frac{J}{E}. \,\! }[/math]

Water Analogy

The relationship between resistivity and resistance can be thought of as a series of pipes. Electrical Resistance in a particular material is similar to an analogy of pipes of varying diameter. The larger the pipe the easier it is for water to get through. The resistivity of the "pipes" never change, but the cross sectional area does, in order for the facilitation of "water" flow (current). If you think about sucking water through a thick straw and a coffee stirrer, it is much more difficult to suck the water using the stirrer. Though the materials both are made of may be the same and the water is the same in each instance (i.e. resistivity), it is harder to use the coffee stirrer because of the smaller cross-sectional area.

Resistivity of Materials

Every conductor has a natural resistivity that is relatively consistent at a given temperature. This number is calculated through experimentation. Here is a list of common conductors and their resistivities.

(http://avstop.com/ac/Aviation_Maintenance_Technician_Handbook_General/images/fig10-41.jpg)

As you can see, silver has a lower resistivity than copper but because silver is the more expensive of the two, copper is the material of choice when making wires for both construction and classroom use.

Temperature

In addition to each material having a different resistivity. The same material at different temperatures may exhibit different resistivities. As materials heat up they become less facilitative of current flow. This is due to the fact that nuclei are moving faster at a sub-atomic level, when this occurs it creates more of a wall which is difficult for electrons to pass through. Because the nuclei do not move as much when the material is colder, it creates less of a "sheet" of nuclei for electrons to pass through.

Examples

Here are a few questions involving resistance and resistivity of differing difficulty.

Simple

Problem 1

An unknown ohmic resistor is attached to a 3V battery and the current is measured at 1 amp. Calculate the resistance of the unknown resistor.

Also, theoretically, if this resistor has a diameter of 0.03m, and length of 0.06m, what is its resistivity?

Solution

Using the equation [math]\displaystyle{ I = \frac{dV}{R} }[/math] we can substitute is 1 for I and 3 for dV leaving us with the equation [math]\displaystyle{ 1 = \frac{3}{R} }[/math]. Solving for R we come to the conclusion that the resistance must be 3 ohms.

To calculate resistivity, we put 7.06E-4m^2 for cross-sectional area, 0.06m for length and 3 ohms for resistance into our equation, getting [math]\displaystyle{ 3 = \frac{\rho 0.06}{7.06E-4} }[/math]. When you solve for resitivity, you get the answer of 254.65 ohms/meter

Middling

Problem 2

A cylinder of an unknown material has a resistance of 30 ohms. Another cylinder made of the exact same material is twice as long and has a radius that is twice as large. What is the resistance of this cylinder?

Solution

Given the equation [math]\displaystyle{ R = \frac{\rho L}{A} }[/math] we know that when the length is doubled the resistance must also double. In addition we know that when the radius is doubled, the cross section area must go up by a factor of 4. This means that the resistance would go down by a factor of 1/4. Putting both of those facts together know that R2 = R1 * 2 * 1/4 or R2 = 15 ohms.

Difficult

Problem 3

A battery and resistor circuit is connected to a very sensitive ohmmeter and is taken outside and left in the sun on a very hot day. What, if anything, will happen to its reading after being outside for a few minutes and why? Assume the battery is unaffected.

Solution

The current would be less that it was inside. Since the circuit was taken outside the resistor would heat up due to the sun. This would in turn cause its resistance to go up. When the resistance goes up and the voltage of the battery stays the same. due to Ohms Law the current must go down, resulting in a lower reading.

Scope

Resistivity is very important to electrical engineers and others who work with circuits because it is important to understand how a circuit is going to work when outside of laboratory conditions. Users cannot expect their circuits to work the same in both nominal and extreme temperature conditions.

2. http://www.britannica.com/technology/resistance-electronics

3. http://www.nist.gov/data/PDFfiles/jpcrd155.pdf

4. http://www.regentsprep.org/Regents/physics/phys03/bresist/default.htm

5. http://forums.extremeoverclocking.com/showthread.php?p=4144637

Resistivity

Contents

The Main Idea

A Mathematical Model

Water Analogy

Resistivity of Materials

Temperature

Examples

Simple

Problem 1

Solution

Middling

Problem 2

Solution

Difficult

Problem 3

Solution

Scope

See also

Further reading

External links

References

Navigation menu