Conservation of Momentum
Claimed by Emily Dunford Edited by Therese Stanley (tstanley6)
- I couldn't figure out how to do in text citations in the wiki so the links at the end of sentences link to the actual links the information was paraphrased from but the references are below in the reference section **
The conservation of momentum is one of the fundamental laws of physics. Within the definitions of a problem, the total momentum of the system stays constant [1]. Much like the conservation of mass or the conservation of energy, the momentum of the objects before the collision is the same as the momentum of the objects after the collision. The momentum is changed through the action of forces [2] as in Newton’s law of motion. This is a powerful idea to solving problems.
The Main Idea
In a system, the total momentum must be conserved. For example, if a collision occurs between 2 objects (object 1 and object 2) in an isolated system, the total momentum of the two objects before the collision is equal to the total momentum of the two objects after the collision [3]. So, the momentum lost by object 1 is equal to the momentum gained by object 2 [4]. However, this does not mean that other aspects of the two objects do not also change. For instance, in an inelastic collision (in which the two objects become entangled), the momentum of object 1 plus the momentum of object 2 before the collision must be equal to the momentum of object 1+2 after the collision. That being said, if the two objects are of equal mass, the velocity of the combined objects will be halved, though the momentum remains conserved because the mass has doubled. The main difference between the conservation of momentum and the conservation of mass or the conservation of energy is that momentum is a vector quantity, so momentum is conserved in the x, y and z directions at the same time [5].
The law of conservation of momentum can be logically derived from Newton’s Third Law [6]. When 2 objects collide, the force on object 1 on object 2 ([math]\displaystyle{ \begin{align} F_1 \end{align} }[/math]) is equal in magnitude and opposite in direction to the force on object 2 on object 1 ([math]\displaystyle{ \begin{align} F_1 \end{align} }[/math]). So: [math]\displaystyle{ \begin{align} F_1=-F_2 \end{align} }[/math]
The objects collide during a certain time period ([math]\displaystyle{ \begin{align} \Delta t \end{align} }[/math]) so that the force acting on object 1 and the force acting on object 2 act over the this time period (Δt). So: [math]\displaystyle{ \begin{align} F_1* \Delta 1 =-F_2* \Delta 1 \end{align} }[/math] We know that [math]\displaystyle{ \begin{align} F*t \end{align} }[/math] is the formula for impulse and since the change in impulse is equal to the change in momentum: [math]\displaystyle{ \begin{align} m_1 * \Delta v_1 = -m_2 * \Delta v_2 \end{align} }[/math] (The Law of Conservation of Momentum).
A Mathematical Model
[math]\displaystyle{ \begin{align} \Delta p_1 = m_1 * \Delta v_1 = -m_2 * \Delta v_2 = \Delta p_2 \,. \end{align} }[/math]
[math]\displaystyle{ \begin{align} p_1 \end{align} }[/math] is the momentum of the first object, [math]\displaystyle{ \begin{align} m_1 \end{align} }[/math] is the mass of the first object, [math]\displaystyle{ \begin{align} v_1 \end{align} }[/math] is the velocity of the first object. [math]\displaystyle{ \begin{align} p_2 \end{align} }[/math] is the momentum of the second object, [math]\displaystyle{ \begin{align} m_2 \end{align} }[/math] is the mass of the second object, [math]\displaystyle{ \begin{align} v_2 \end{align} }[/math] is the velocity of the second object.
A Computational Model
The link below shows a simulation of an elastic collision where one object transfers all of its momentum to the second object after the collision.
Examples
Simple
You are playing pool with your friends at Tech Rec. Two cue balls collide in a head-on collision. Both cue balls have equal mass of 0.165 kg. Before the collision, the first ball is travelling at 9.8 meters per second and the second ball is stationary, 0 meters per second. After the collision, the first ball travels at a velocity of 2 meters per second. What is the velocity of the second ball?
Solution: [math]\displaystyle{ \begin{align} m_1 = m_2 = m = 0.165 \,. \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_1i = 9.8 \,. \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_1f = -2 \,. \end{align} }[/math]
[math]\displaystyle{ \begin{align} V_2i = 0 \,. \end{align} }[/math]
[math]\displaystyle{ \begin{align} m * (v_1f - v_1i)= m (v_2f - v_2i) \,. \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_2f = v_1f - v_1i + v_2i = 9.8 + 2 - 0 = 11.8 \,. \end{align} }[/math] The velocity of the second ball is 11.8 meters per second in the positive x direction.
Medium Difficulty
You are looking out the window of your dorm when you see a person on a Hoverboard collide with a person on a bike. The person on bike was going west with velocity 9 m/s and the person on the Hoverboard was traveling at 30 degrees north of west with velocity 5 m/s. After the collision, both the person on the Hoverboard and the person on the bike become entangled and travel together at some velocity [math]\displaystyle{ \begin{align} v_f \, \end{align} }[/math]. Find [math]\displaystyle{ \begin{align} v_f \, \end{align} }[/math] (See Figure 1 Below)
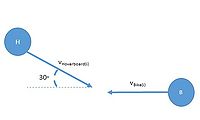
Solution: [math]\displaystyle{ \begin{align} v_H=[9*cos(30), 9*sin(30), 0] \, \end{align} }[/math] [math]\displaystyle{ \begin{align} v_B=[-5,0,0] \, \end{align} }[/math]
[math]\displaystyle{ \begin{align} m_H = 60 kg \, \end{align} }[/math] [math]\displaystyle{ \begin{align} m_B = 50 kg \, \end{align} }[/math]
[math]\displaystyle{ \begin{align} m_H*v_H + m_bike*v_B = (m_H+m_B)*v_final \, \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_f= (m_H*v_H + m_B*v_B)/ (m_H+m_B) \, \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_f = [-1.5155, -4.8503, 0] \,. \end{align} }[/math] m/s
Difficult
During a baseball game the 0.145 kg baseball is thrown straight upward with a velocity of 40 m/s. What is the recoil velocity of the earth? Why don’t we notice that the earth has gained velocity?
Solution: [math]\displaystyle{ \begin{align} m_b = 0.145 kg \, \end{align} }[/math] [math]\displaystyle{ \begin{align} m_E = 5.972 e 24 kg\, \end{align} }[/math] [math]\displaystyle{ \begin{align} v_b = 40 m/s \, \end{align} }[/math]
The system is the baseball plus the earth. So, the total momentum of the system must be conserved (i.e. the momentum before must be equal to the momentum after.)
[math]\displaystyle{ \begin{align} m_b*v_b=-m_E*v_E .\, \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_e= - (m_b*v_b)/m_E .\, \end{align} }[/math]
[math]\displaystyle{ \begin{align} v_e=- 9.7120e-25 m/s .\, \end{align} }[/math]
Even though the magnitude of the momentum of the ball equals the magnitude of the momentum of the Earth, the Earth’s mass is so massive that the Earth recoils with a velocity so small we don’t feel it.
Real World Connection
The Conservation of Momentum is prticularly important in fluid flow and transport. In the field of biomedical engineering, engineers are often times working with fluids flowing through the body. So when a new design for a pacemaker is made, engineers need to find out how the new pacemaker diverts fluid flow in the body. To solve a problem like this, one would use Reynold's Transport Theorem, as well as the principle of conservation of momentum as a result of the basis for Reynold's Transport Theorem being the principles of Conservation of Mass and the Conservation of Momentum. No new device can be made for the human body without such an analysis. In addition, in certain disease states such as atherosclerosis, when certain arteries become clogged, the fluid flow is diverted and there is a change in pressure. To model certain situations, engineers would start from basic principles such as Conservation of Mass and Conservation of Momentum.
In this way, the Conservation of Momentum (as well as the Conservation of Mass and the Conservation of Energy) plays an important roles in engineering fields, such as Biomedical Engineering. These conservation law are also important in other engineering fields. To name a few examples, Chemical engineers are concerned with fluid flowing through a pipe, and mechanical engineers are concerned with fluid flowing through an engine.
History
Newton established the Conservation of Momentum along with the other Conservation Laws (except Conservation of Energy). Newton published his theories in 1687 in Philosophiæ Naturalis Principia Mathematica (linked below in external links) [8]. When Newton was publishing his work, the challenge that he faced was describing his theories without using calculus. Newton did not publish his La Methode Dex Fluxions until 1736 [9]. Newton's work on momentum was mostly focused on forces rather than energy and vectors[10].
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
For extra concept quetions see: [11]
External links
Newton's Philosophiæ Naturalis Principia Mathematica: [12]
References
1. "Conservation of Momentum." Conservation of Momentum. NASA, 05 May 2015. Web. 05 Dec. 2015. <https://www.grc.nasa.gov/www/k-12/airplane/conmo.html>.
2. "Momentum Conservation Principle." Momentum Conservation Principle. The Physics Classroom, n.d. Web. 05 Dec. 2015. <http://www.physicsclassroom.com/class/momentum/Lesson-2/Momentum-Conservation-Principle>.
3. Smith, George. "Newton's Philosophiae Naturalis Principia Mathematica." Stanford University. Stanford University, 20 Dec. 2007. Web. 05 Dec. 2015. <http://plato.stanford.edu/entries/newton-principia/>.
4. "Mathematical Treasure: Newton's Method of Fluxions." Mathematical Treasure: Newton's Method of Fluxions. Mathematical Association of America, n.d. Web. 05 Dec. 2015. <http://www.maa.org/press/periodicals/convergence/mathematical-treasure-newtons-method-of-fluxions>.