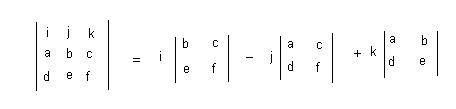Right Hand Rule

This topic covers Right Hand Rule. Claimed by: Layla Darian

The Main Idea

The magnitude of the translational angular momentum doesn't tell us everything about the motion of an object. For example, to describe the motion of Earth's orbit if you are standing on the positive z axis looking toward the origin, the Earth is moving counterclockwise in the xy plane. However, this statement cannot be used mathematically. You can't add "counterclockwise in the xy plane" to "clockwise in the yz plane." Instead, we can use the right hand rule to describe the direction of angular momentum as a vector. The direction can be specified like this:

The plane in which both the position vector from the two objects and the momentum vector for the object of interest lie can be indicated by a unit vector perpendicular to that plane.
The direction of motion within the plane (clockwise or counterclockwise) can be indicated by establishing a right hand rule (RHR) for this unit vector.

Visualization

You can use your right hand to visualize the intuition of the Right Hand Rule. Consider the x-y-z space drawn with these axes from the origin:

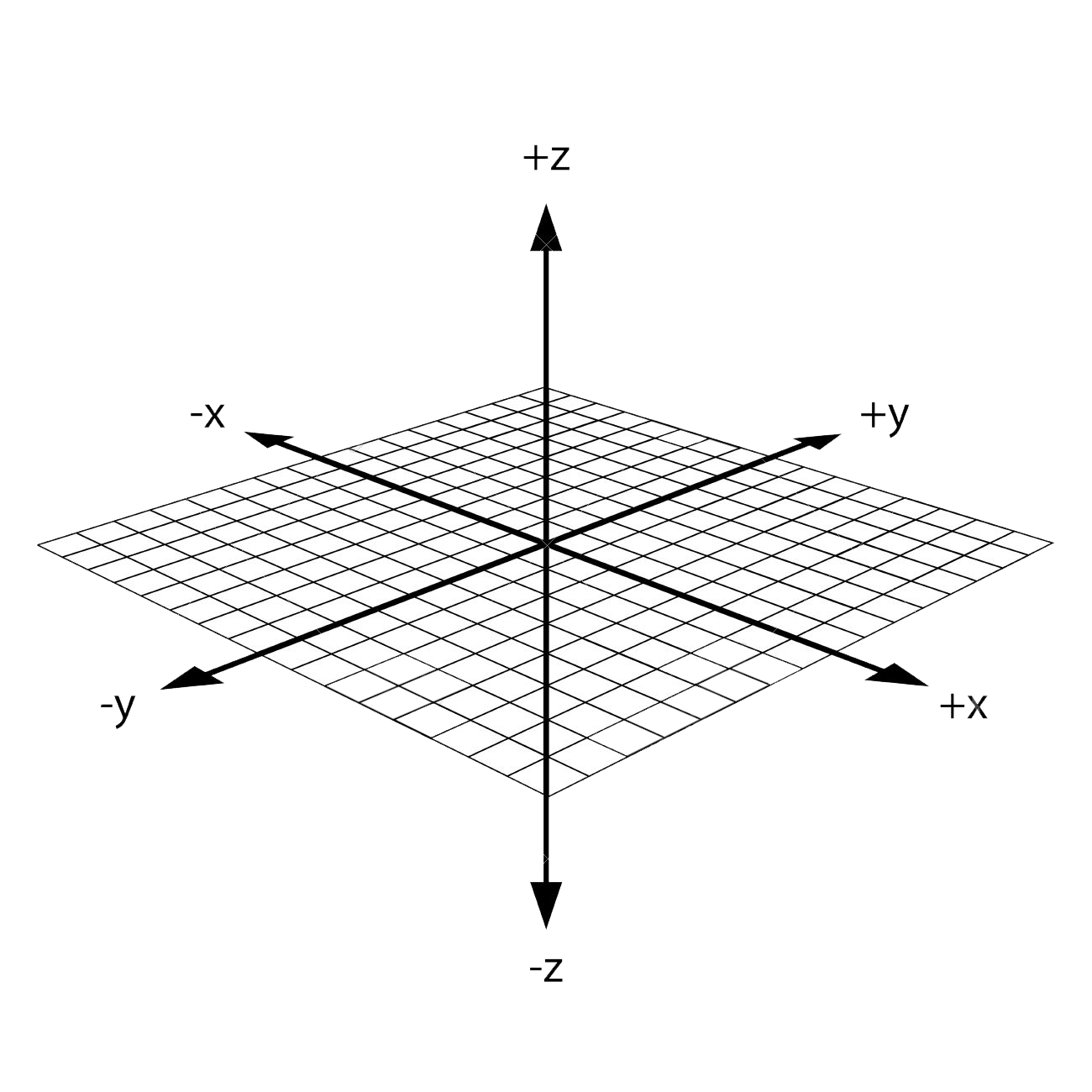
Now, take your right hand and point your index finger forward (the direction your arm faces), point your thumb up, and point your middle finger perpendicular to your index finger. Your thumb is the z-axis and points in the positive z-direction. Your index and middle fingers represent the x-y plane. Your hand should look something like this:

Now visualize the x-y-z axes over your hand like this: File:Right hand directions.png

Realize that you can rotate the x-y plane along the z-axis. For example, if you were to rotate the original x-y plane 90 degrees clockwise, you would see this:

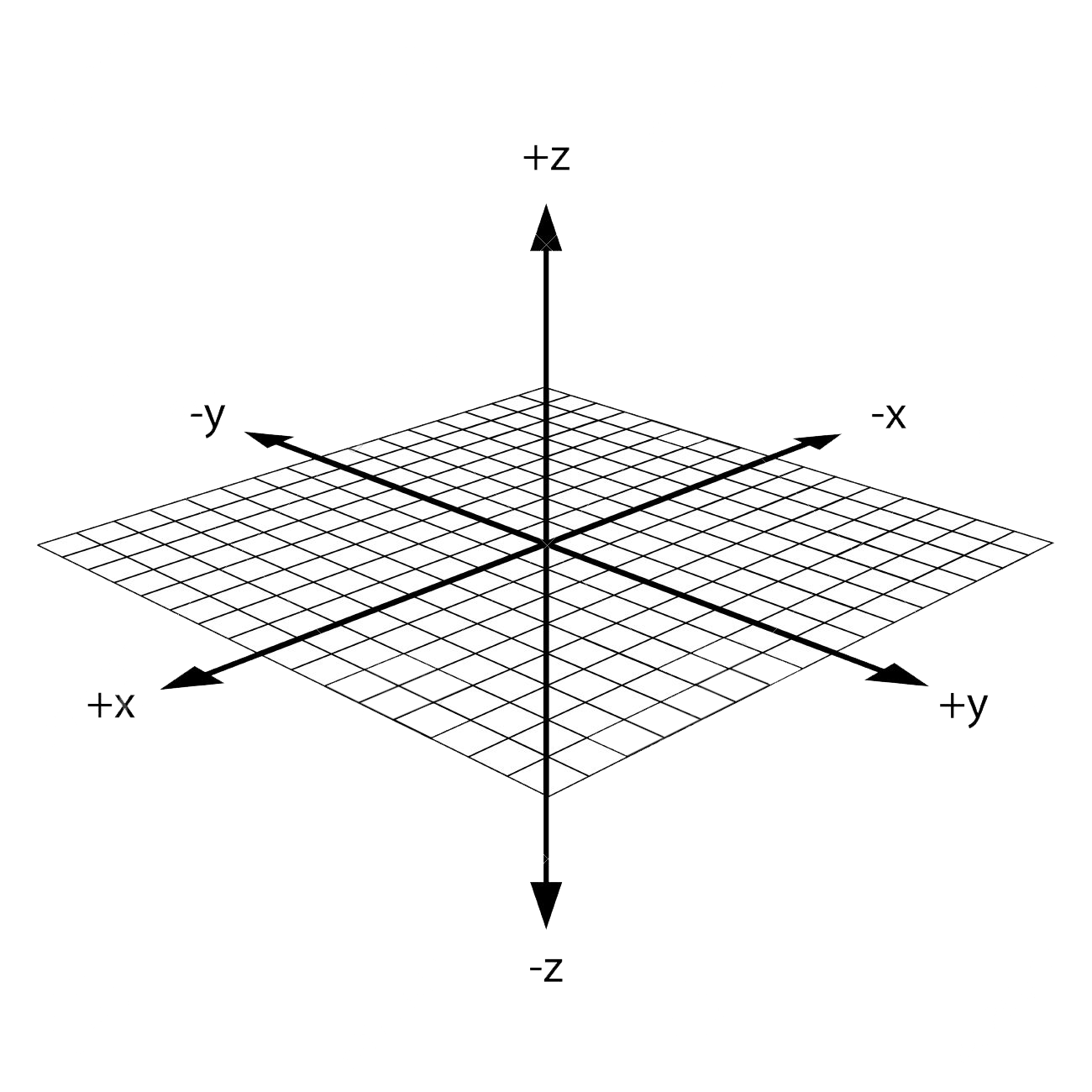
Rotate the plane once more 90 degrees clockwise:

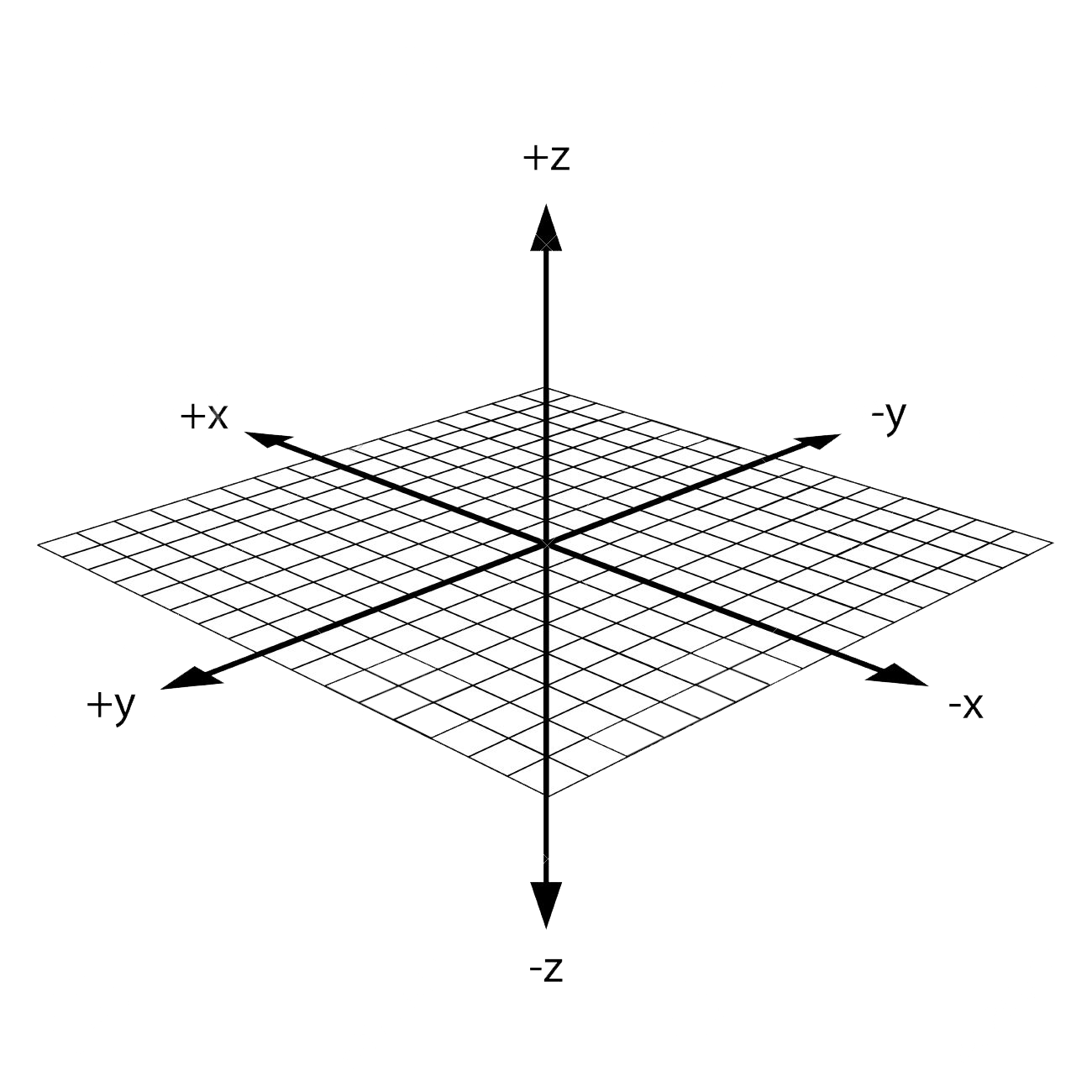
Now, as you can see, your right hand indeed represents the entire x-y-z space. File:Right hand axis.png

Performing the Right Hand Rule

Right Hand Rule: Using your right arm, point your arm to represent the "r" vector. Now turn your palm in the direction of the momentum vector. Curl your fingers in that direction of the momentum, and extend your thumb outward. The unit vector representing the direction of the angular momentum is defined to point in the direction of your thumb.
Hint: If the rotational motion is counterclockwise, your right thumb, therefore the unit vector, will point out of the plane. If the rotational motion is clockwise, the unit vector will point into the plane.

Counterclockwise example: File:Counterclockwise example.png Notice your thumb points up in the +z direction when the direction from "r" to "p" is counterclockwise.

If the "p" vector is in the other direction relative to "r", you would need to turn your hand upside down to curl your fingers towards it. In this case, your thumb points down in the -z direction!

This situation would also make your thumb point in the -z direction (Notice it is just the first image rotated 180 degrees).

A Mathematical Model

The direction of the angular momentum can also be solved through calculating the cross product of the r and p vectors. The cross product of two vectors can be solved as so:

The first row is the standard basis vectors and must appear in the order given here. The second row is the components of r and the third row is the components of p. First, the terms alternate in sign and notice that the 2x2 is missing the column below the standard basis vector that multiplies it as well as the row of standard basis vectors. To solve for the "i" component, you use the expression: bf - ce. Do the same for the "j" and "k" components, and this will give you your vector. Your vector should be <bf-ce, af-cd, ae-bd>.

For more on the explanation of how to calculate cross product, visit this website: https://www.mathsisfun.com/algebra/vectors-cross-product.html

Here is an example problem. Solve first using the right hand rule, and then solve mathematically with the cross product.

Answer: The cross product should be <-12, 0, 0> So the vector is in the -x direction, which the right hand rule also tells us.

Examples

Ans: 4

Ans: 3

Ans: L(A)=L(B)=L(H) = <0, 0, -30> L(G)=L(C) = <0, 0, 0> L(D)=L(E)=L(F) = <0, 0, +50>

Connectedness

Right Hand Rule is essential for solving all angular momentum problems. Angular Momentum has been my favorite topic so far this semester. I think the problems and situations are very interesting, and they explain the reason behind why a lot of stuff in real life happen that we don't generally think about.

Here are some interesting videos about the conservation of angular momentum:

https://www.youtube.com/watch?v=Aw5i994n2bw&feature=youtu.be

https://www.youtube.com/watch?v=OKbawIq3w7U

History

I wasn't able to find who was the first to apply the Right Hand Rule to angular momentum and torque. However, it seems that the right hand rule is applied to other aspects of physics as well. For example, André-Marie Ampère, a French physicist and mathematician, created a right hand rule for circuits and electric currents. This is used when a vector must be defined to represent the rotation of a body, a magnetic field, or a fluid. It reveals a connection between the current and the magnetic field lines in the magnetic field that the current created. This right hand rule works exactly the same way as the one I have described above.

References

All pictures and videos were taken from Professor Flavio Fenton's Physics 2211 lecture notes. https://en.wikipedia.org/wiki/Right-hand_rule