Speed of Sound in Solids
CLAIMED BY ANTHONY CHAWKI This page discusses calculating the speed of sound in various solids and provides examples of such calculations.
The Main Idea
The speed of sound is the speed that sound waves travel through a particular medium. The medium determines the speed limit. Mediums are composed of particles that could be closely knit together or relatively spread apart. Also, these particles could act elastic or inelastic. The closer together the particles are to each other the faster the sound can be transferred through the medium. In comparison to air, sound travels considerably faster in solids. The factors that control the speed that sound travels in various solids is measured by the solid's density and elasticity, as these factors effect the vibrational energy of the sound.
With an increase in density, the space between particles in the solid decreases. The smaller distance between particles, or interatomic distance, the higher the speed. With an increase in elasticity of the atoms that make up the object, the lower the speed of sound in the object. Particles that have a high elasticity take more time to return to their place once they received vibrational energy. However, if the solid is completely inelastic then the sound cannot travel through it.
The practicality of this concept is great. Everyday humans' ears capture sound waves through the Pinna,
or the outer cartilage piece of the ear. The sound waves then travel up the ear canal and hit the ear drum, which vibrates from the sound. The vibrations travel through the inner ear and end up at the Cochlea. The Cochlea transfers the vibrations into information that the auditory nerve can analyze. This process occurs everyday and without proper education of sound traveling through solids, such as the ear's different pieces, humans wouldn't be able to completely understand the concept completely.
A Mathematical Model
The speed of sound in solids [math]\displaystyle{ {V_{s}} }[/math] can be determined by the equation. Young's Modulus is a measure of elasticity of an object, and it can be computed to solve for interatomic values, such as interatomic bond stiffness or interatomic bond length.
[math]\displaystyle{ {V_{s}} = d* √ (K_{s}/m_{atom}) }[/math]
Alternative speed equation:
[math]\displaystyle{ {V_{s}} = √ (B/ρ) }[/math]
[math]\displaystyle{ ρ }[/math] = density
[math]\displaystyle{ B }[/math] = Bulks Modulus
Bulks Modulus = [math]\displaystyle{ {\frac {ΔP}{ΔV/V}} }[/math]
[math]\displaystyle{ d }[/math] = interatomic bond length
[math]\displaystyle{ K_{s} }[/math] = Interatomic bond stiffness
Youngs Modulus = ([math]\displaystyle{ Y = K_{s}/d }[/math])
Youngs Modulus: [math]\displaystyle{ Y ={\frac{Stress}{Strain}} }[/math]
[math]\displaystyle{ Stress = {\frac{F_{tension}}{Area_{Cross Sectional}}} }[/math]
[math]\displaystyle{ Strain = {\frac{ΔL_{wire}}{L_{0}}} }[/math]
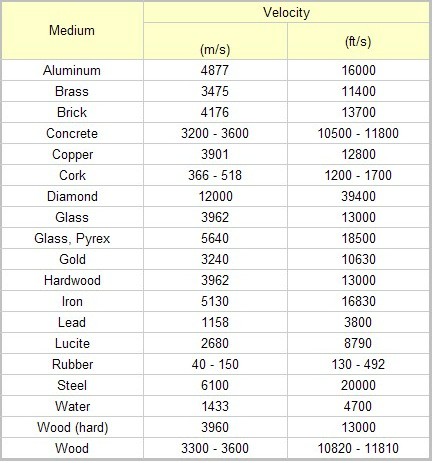
Speeds of Various Compositions
Examples
Theoretical
Two metal rods are made of different elements. The interatomic spring stiffness of element A is four times larger than the interatomic spring stiffness for element B. The mass of an atom of element A is four times greater than the mass of an atom of element B. The atomic diameters are approximately the same for A and B. What is the ratio of the speed of sound in rod A to the speed of sound in rod B?
Solution: In this situation, the ratio of the speed of sound in rod A to the speed of sound in rod B is 1.
Looking at the formula for computing speed of sound in solids, [math]\displaystyle{ {V_{s}} = d* √ (K_{s}/m_{atom}) }[/math], you see that velocity depends three factors, interatomic stiffness, the mass of one atom, and interatomic bond length. The two rods differences in atomic mass and interatomic stiffness offset each other when the equations are set equal, and the ratio is determined to be 1.
[math]\displaystyle{ d* √ 4(K_{s}/m_{atom}) = d* √ (K_{s}/4m_{atom}) }[/math] After simplification [math]\displaystyle{ V_{s_{1}} = V_{s{2}} }[/math]
Numerical Example
The Young's Modulus value of silver is 7.75e+10, atomic mass of silver is 108 g/mole, and the density of silver is 10.5 g/cm3. Using this information, calculate the speed of sound in silver.
Solution: The key to solving this problem is to realize the micro-macro connection of Young's Modulus. You are given that Young's Modulus is equal to 7.75e+10, and we know that Youngs Modulus = ([math]\displaystyle{ K_{s}/d }[/math]). In this situation, we need to calculate the interatomic bond length and use it and our Young's Modulus value to determine our interatomic stiffness.
To solve for d, we use the given density of silver (10.5 g/cm3). Using the basic equation for volume in relation to density and mass ([math]\displaystyle{ V=m*d }[/math]), we can find d, since d is equal to the cube root of volume.
Once d is solved for, it can be plugged back into the the equation [math]\displaystyle{ Y = K_{s}/d }[/math] to solve for [math]\displaystyle{ K_{s} }[/math]
Now, we have solved for both interatomic bond length and stiffness. The only quantity in the final speed of sound equation we need is the mass of one atom, which can be determined using Avogardro's number and the atomic mass. [math]\displaystyle{ m_{atom} = }[/math] atomic mass / [math]\displaystyle{ 6.022e23 }[/math]
Now that all variables are solved for, we can substitute values into our [math]\displaystyle{ {V_{s}} = d* √ (K_{s}/m_{atom}) }[/math] equation.
[math]\displaystyle{ {V_{s}} = 1.6e-10* √ (78534.7/1.79e-22) }[/math]
[math]\displaystyle{ {V_{s}} = 2723 }[/math] m/s
Connectedness
The computation of speed of sound in solids is dependent on a mass' interatomic properties, such as interatomic bond length. I find it interesting when a object's interatomic properties determine its functionality on a larger scale. In the case of speed of sound in solids, the objects elasticity depends on the interatomic bond length.
While the computation of speed of sound in solids may not seem related to Industrial Engineering, it has clear implications in the process of choosing building materials, which is a notable section of industrial engineering. For example, if you are planning to build something soundproof, it would be optimal to choose a solid with a very low speed of sound velocity.
The industrial applications in terms of construction are vast. An objects ability to block/allow sound waves through it is very important. Of course, insulation materials and sound proof wall materials come to thought at first. However, in some cases, contractors need to build structures that allow sound to travel through, in which they would choose solid materials that correlate with high speeds of sound.
History
The speed of sound in air was first measured by Sir Isaac Newton, and first correctly computed by Pierre-Simon Laplace in 1816. Before this precise measurement, attempts had been made across Europe during the 1700s, most famously Reverend William Derham's experiment in 1709 across the town of Upminister, England. Reverend Derham used a shotgun's noise and several known landmarks around time to measure the time it took for the sound of the blast to be heard from select distances.
Young's Modulus was named after English physicist Thomas Young. In actuality, the concept was developed earlier by physicists Leonhard Euler and Giordano Riccati in the 1720s.
See also
Youngs Modulus: [1] Interatomic Bonds: [2]
Further reading
Further Information can be found on the speed of sound in solids in Matter and Interactions, 4th Edition by Ruth W. Chabay & Bruce A. Sherwood
External links
Internet resources on this topic can be found at:
Engineering Tool Box [3]
Hyperphysics [4]
Potto Project [5]
NDT Resource Center [6]
The Engineering ToolBox [7]
Ear Image [8]
Yew Chung [9]
References
This section contains the the references used while writing this page
Chart from [10]
Matter and Interactions 4th Edition by Chabay and Sherwood
Wikipage created by Daiven Patel