Inductors

Short Description of Inductors Rohan Mundkur (Fall 2016)

Inductors - Conceptual Overview

An inductor's broad purpose, within circuits, is to resist changes in current. Upon examining the structure and characteristics of inductors, we are able to develop mathematical and conceptual arguments that explain this behavior. Inductors typically consist of a conductor, usually wire, wrapped in a coil.

The conductor that makes up the inductor will have a current running through it, and as this non-changing current runs, a magnetic field will be created within the center of the coil. Therefore, as the current begins to change, the respective flux through a ring of the coil will change as well. As we know, the ratio of a change in flux to the respective change in time will provide us with the potential difference resulting from the change in current. By multiplying this potential difference by the number of loops in the circuit, we are able to obtain the coil's overall potential difference due to the single change in current.

The essential directional behavior of the induced emf is to be opposite the coil's magnetic field when the current increases and in line with the coil's magnetic field when the current decreases. We can make this assumption because if the behaviors were reversed, any change in current would result in an infinite increase or decrease. This phenomenon occurs because of the direction of the non-Coulomb (NC) electric field's direction in relation to the Coulomb electric field's direction (direction of current). When the current through the inductor increases, the NC electric field curls in the opposite direction of the current, but when the current through the inductor decreases, the NC electric field curls in the same direction as the current.

The mathematical characterization of this phenomenon will be described in greater detail below.

Mathematical Model and Explanation

As we established earlier, an inductor's emf has roots in ratio of change in flux to change in time. We most often look at solenoids when discussing inductors, so the explanations and diagrams below will be solenoid specific though the concepts can be applied to coils with any shape - this is the case as flux is dependent on area.

The derivation below begins by providing the formula for the magnetic field within a solenoid and continues by applying this magnetic field (and subsequent changes due to change in current) to the equation for flux given the solenoid is comprised of "N" rings with radius "R". After determining the emf of a single loop, we multiply by "N" to obtain the emf of the entire solenoid. Finally, in order to simplify our expression and provide a segway to the exploration of non-solenoid inductor shapes, we represent the proportion of total emf to change in current by the variable "L" whose units are henries (H).

Examples

Simple

If a solenoid is filled with iron, will it have a higher or lower inductance?

Answer: The solenoid will have a higher inductance, because the permeability constant has changed to the value of permeability of iron, which is much higher than that of free space. Therefore, the inductance will be higher with an iron core than with an air core.

Middling

A 5 meter solenoid with 500 turns of copper wire creates an emf with a magnitude of 20V when current increases by 10 Amps/second. What is the radius of the coil?

We begin with our simplified expression and begin algebraic rearrangements to create an expression that provides us with a value for "R". After this, we simply plug in the values we are given, and compute our radius.

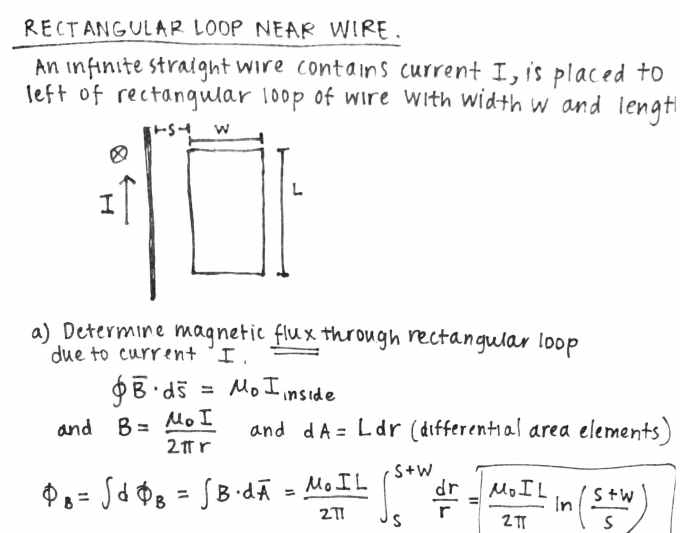
Difficult

This problem is taken from this website: http://www.physics.umd.edu/ However, it is a great problem that delves into the difficulty of solving induced emf problems, since it can be more than just plugging in variables.

Connectedness

How is this topic connected to something that you are interested in?

Self-inductance is extremely interesting because it counteracts the "previous" current. This means that there are many applications of it. For instance, you can use it in electric generators, electric motors, electric guitars, and transformers.

Is there an interesting industrial application?

Yes, there is! Ever heard of an inductive loop detector? It's how traffic is controlled at some intersections. Basically, inductive loop detectors (ILD's) are located underneath the pavement. When a car passes, it acts as a conductor, and changes the inductance of the loop of conducting wire. The change in inductance is used to detect cars above, and thereby used to control traffic with the traffic signals.

How is it connected to your major?

Self inductance does not directly relate to my major, which is biochemistry. However, there is a concept called the "inductive effect," which is similar in the way that it works. It is the electronic effect due to the polarization of σ bonds within a molecule. This is because of the electronegativity difference between the atoms at the ends of the bond.

Also, self-inductance is the change in electric current in a coil, and electrons and their effects are studied under chemistry. This would be known as physical chemistry.

History

What are the units of inductance, you may ask? Henries! A term named after Joseph Henry, an American scientist. Interesting fact: He discovered electromagnetic induction independently, but at the same time as Michael Faraday. Faraday just got a lot of the credit because he published a lot of papers first. However, Henry did discover mutual inductance and self inductance.

Inductors

Contents

Inductors - Conceptual Overview

Mathematical Model and Explanation

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu