Bohr Model

Sherry Guo (Spring 2017)

This page gives basic information about the Bohr model and quantization. It also includes examples using the Bohr model.

Main Idea

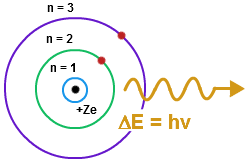
The Bohr model of the atom was proposed by Niels Bohr in 1913, and it was radically different from any other models that previously existed. His model depicted atoms as having negatively charged electrons which orbited as small, positively charged nucleus. Bohr's incorporation of quantum theory was the most groundbreaking part; in this model, electrons can only exist in discrete energy levels, which are quantized. This model is very simplistic and is useful in introducing students to quantum mechanics. Although this model successfully predicts energy levels of the hydrogen atom, it has its shortcomings.

Bohr's Assumptions

Electrons travel in a circular orbit around the nucleus, similar to how planets orbit around the sun.
The energy that electrons have is related to their distance from the nucleus, or which energy level they occupy. The further away the electron, the more energy it has.
Electrons can gain or lose energy by jumping from one orbit to another. The energy is quantized - the orbitals have discreet radii.
When an excited electron returns back to its ground state, then it releases the energy that it absorbed, in the form of light. This quantized energy is equal to the difference between the energies of the orbits.

History

] Ernest Rutherford proposed that the basic structure of an atom is a cloud of electrons which surround a small nucleus. With his experiments, he developed a model that depicted an atom like a solar system, with electrons orbiting around the nucleus. He proposed that the emission spectrum of hydrogen would look more like a smear rather than being made up of distinct lines. However, this was flawed, as it suggested that atoms can emit energy that isn't quantized. [8]

Niels Bohr was able to explain the emission spectra of hydrogen by improving on the Rutherford model of the atom. Bohr noticed that in the atomic emissions spectrum of hydrogen, only certain colors could be seen. Thus, he theorized that electrons need to be in energy levels that are quantized. He related the energies of the colors he saw to the differences of hydrogen's energy levels. Although this model is not entirely correct, as it only applies to systems where two charged particles orbit each other, it still has many features that are very applicable to physics today. [9]

Shortcomings of the Bohr Model

While the Bohr model is an important predecessor to the current quantum mechanical models of the atom, it doesn't correctly describe some aspects of electron orbitals. It does not provide any reasoning as to why certain spectral lines are brighter than others. Its main shortcoming is that it violates the uncertainty principle, as it considers electrons to have a definite radius and momentum. This model is very basic, and in order to know more specific details about spectra and charge distribution, more calculations must be done. Many of the failures of the Bohr model can be corrected by the Schrodinger equationfor the hydrogen atom.

Application

A Mathematical Model

The Angular Momentum Quantum

[math]\displaystyle{ ħ = h/2π =1.05*10^{-34} J*s }[/math] h is Planck's constant, which is a physical constant that is essential in quantum mechanics.

Angular Momentum Is Quantized

[math]\displaystyle{ |\vec L_{trans,C}| = rp = Nħ }[/math]

p is the electron's momentum r is the radius of circular orbit N is an integer (1,2,3, ...)

We can derive the equation for r, the allowed Bohr radii for electron orbits.

1) Electric force the proton exerts on the electron: [math]\displaystyle{ F_{el} = {\frac{e^2}{4π ε0 r^2}} }[/math]

2) Using the momentum principle and curving motion: [math]\displaystyle{ |F_{perpendicular}| = {\frac{|p| |v|}{r}} = {\frac{e^2}{4π ε0 r^2}} }[/math]

3)Substituting in Bohr's conditions: [math]\displaystyle{ {\frac{N^2 h*^2}{mr^3}} = {\frac{e^2}{4π ε0 r^2}} }[/math]

4)Solving for the allowed radii [math]\displaystyle{ r = {\frac{4π ε0 h*^2}{me^2}} *N^2 }[/math] where N = 1,2,3,...

Additionally, the formula for energy of hydrogen atom of different levels is also derived from this model.

E = K + Uelectric

1) [math]\displaystyle{ E = {\frac{mv^2}{2}} - {\frac{{\frac{1}{2}}*{\frac{1}{4π ε0}}*{\frac{me^2}{h*}}}{N^2}} }[/math]

2) [math]\displaystyle{ E = {\frac{13.6 eV}{N^2}} }[/math] where N = 1,2,3

A Computational Model

To interact with this glowscript visualization of the Bohr Model, click here. You will also find a graph of Energy (eV), Kinetic Energy, and Potential Energy. This visualization shows how the electrons jump from level to level according to the Bohr Model. There is also an energy vs distance graph shown which varies according to these levels. Notice that the further away the electron is, the more energy it has.

Examples

Simple

How much energy in electron volts is required to ionize a hydrogen atom, if initially the atom is in the state N = 3? Here we can use the formula for the hydrogen atom which is

1) [math]\displaystyle{ E = {\frac{-13.6 eV}{N^2}} }[/math]

2) [math]\displaystyle{ ={\frac{-13.6 eV}{3^2}} }[/math] = -1.51 Joules

Middling

[6]A hydrogen atom is in state N = 3, where N = 1 is the lowest energy state. What is K+U in electron volts for this atomic hydrogen energy state?

1) [math]\displaystyle{ E(3) = {\frac{-13.6 eV}{3^2}} }[/math] = -1.51 Joules

2) [math]\displaystyle{ E(1) = {\frac{-13.6 eV}{1^2}} }[/math] = -13.6 Joules

3) K+U = energy of photon = [math]\displaystyle{ E(1) - E(3) = {\frac{-13.6 eV}{3^2}} - {\frac{-13.6 eV}{1^2}} }[/math] = 12.09 Joules

To the right is the graph of E as the hydrogen atom goes from N = 3 to N = 1.

Difficult

Hydrogen has been detected transitioning from the 101^st to the 100^th energy levels. What is the wavelength of the radiation? Where in the electromagnetic spectrum is this emission?

To solve this problem, we first need to use formulas derived from Bohr Model of hydrogen atom. It is [math]\displaystyle{ E = {\frac{-13.6 eV}{N^2}} }[/math]

Then solve for the wavelength using formula from Electromagnetic Wave Theory.

This wavelength falls in the microwave portion of the electromagnetic spectrum.

Connectedness

This topic is quite interesting as it is the initial introduction to quantum physics, which I find particularly intriguing. Although, this model has had shortcomings, it is one of the most successful models of its time. It has many features that are used in the actual model for quantum physics. This model also involves coding to show the visualization, which is how it somewhat related to Computer Science. Additionally, there are quite a few applications of the Bohr's Model. Bohr's discovery of the quantum leap is, in many ways, the most shining example of the consequences which Bohr's model of the atom has had for modern society. Bohr's notion that atoms emit light quanta with very specific energies is behind many of the technologies on which we depend our daily lives. Laser technology, which is becoming very popular in today's world, depends entirely on principles behind Bohr's model of atom because laser light is produced by quantum leaps. The quantum leaps between the specific energy levels show that light has specific frequency and wavelength which measures time and length precisely. However, due to shortcomings in Bohr's Model, we can't completely utilize these calculations, but the framework is used.

[1] [2] [3] [4] [5] [6] [7] [8] [9]