Point Charge

This page is all about the Electric Field due to a Point Charge.CLAIMED BY DEJAN TOJCIC 10-31-2016 == Electric Field==

A Work In Progress by Dejan Tojcic. dtojcic3 (talk)

The Main Idea

Looking at one of the four fundamental interactions of physics, electromagnetism, you can derive the expression for Coulombs Force Law. Using this expression, there is just a simple equation that is used to derive the the exact value of the electric field. The electric field of a point charge can be directly coordinated with a couple of independent variables. The variables that are directly coordinated with the value of an electric field is the direction of the particle and the charge of the particle. Electric field of a point charge is also inversely proportional to distance.

A Mathematical Model of Electric Field due to Point Charge

The Electric Field of a Point Charge can be found by using the following formula:

[math]\displaystyle{ \vec E=\frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} \hat r }[/math]

[math]\displaystyle{ Where \frac{1}{4 \pi \epsilon_0 } \text{is a constant representing the permittivity of free space, and is approximately } 9*10^{9} \frac{N m^2}{C^2} }[/math] , r is the magnitude of the distance between the observation location and the source location , q is the charge of the particle and [math]\displaystyle{ \hat r \text { is the direction of the distance from the source location to the observation point.} }[/math]

It is very easy to derive Coulombs Law using the equation for the electric field of a point charge, as all you have to do is multiply the value obtained from the Electric Field of a point charge by the charge of the second particle.

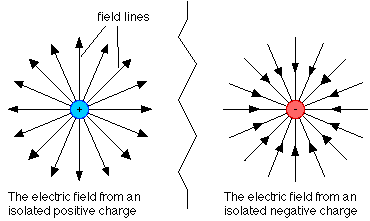
Below is a visual representation of electric fields due to a positive and negative point charge

A Computational Model

Here is a link to some code which can help visualize and compute the Electric Field due to an electron at different points. You can adjust the values of the observation locations in order to observe how the effects of distance, both magnitude and direction, can affect the electric field.

https://trinket.io/glowscript/8d66c87ced

Examples

Simple

There is an electron at <0,0,0>m. Calculate the electric field at <4,-3,1>m.

Step 1: Find [math]\displaystyle{ \hat r }[/math]

Find [math]\displaystyle{ \vec r_{obs} - \vec r_{electron} (\lt 4,-3,1\gt - \lt 0,0,0\gt = \lt 4,-3,1\gt }[/math]m

Calculate the magnitude of r. ([math]\displaystyle{ \sqrt{4^2+(-3)^2+1^2}=\sqrt{26} }[/math]

From r, find the unit vector [math]\displaystyle{ \hat{r}. }[/math] [math]\displaystyle{ \lt \frac{4}{\sqrt{26}},\frac{-3}{\sqrt{26}},\frac{1}{\sqrt{26}}\gt }[/math]

Step 2: Find the magnitude of the Electric Field

[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} = \frac{1}{4 \pi \epsilon_0 } \frac{-1.6 * 10^{-19}}{26} }[/math]

Step 3: Multiply the magnitude of the Electric Field by [math]\displaystyle{ \hat{r} }[/math] to find the Electric Field

E= [math]\displaystyle{ \frac{1}{4 \pi \epsilon_0 } \frac{-1.6 * 10^{-19}}{26}*\lt \frac{4}{\sqrt{26}},\frac{-3}{\sqrt{26}},\frac{1}{\sqrt{26}}\gt =\lt -4.34*10^{-11},3.26*10^{-11},-1.09*10^{-11}\gt N/C }[/math]

Middling

A particle of unknown charge is located at <-.21, .02, .11> m. Its electric field at point <-.02, .31, .28> m is <.124, .188, .109> N/C . Find the value of the particles charge.

While this problem looks challenging, lets think about it for a second. We are given both an observation location and a source location, so we can find both r and [math]\displaystyle{ \hat{r} }[/math] Since we are given the value of the electric field, we can simply find the magnitude of the electric field. Then, we can use the equation for the magnitude of electric field of a point charge,[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math] to find the charge.

Step 1: Find [math]\displaystyle{ \vec r_{obs} - \vec r_{particle} \lt -.02,.31,.28\gt m - \lt -.21,.02,.11\gt m = \lt .19,.29,.17\gt m }[/math]

To find r_{mag}, we simply find the magnitude of <.19,.29,.17>.

([math]\displaystyle{ \sqrt{.19^2+.29^2+.17^2}=\sqrt{.1491} }[/math]= .39

Step 2: Find the magnitude of the Electric Field

E= <.124, .188, .109> N/C

E_{mag} = ([math]\displaystyle{ \sqrt{.124^2+.188^2+.109^2}=\sqrt{.0626} }[/math]=.25

Step 3: Find q by rearranging the equation for E_{mag}

[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math]

By rearranging this equation we get

[math]\displaystyle{ q= {4 pi epsilon_0 } *{r^2}*E_{mag} }[/math]

[math]\displaystyle{ q= {1/(9*10^9)} *{.39^2}*.25 }[/math]

q= 4.3*10^-12 C

Difficult

The electric field at a location <.5.4, -1.8, 7.2>m has been found to be <5.5*10^3, -7.6*10^3, 0> N/C. There is a particle with a charge of -2nC in the surrounding area. What is the location of the particle?

Again, while at first sight the problem may look tough, it is really not that difficult once you break it down. Since we are given the vector value for electric field, we can also find the magnitude of the electric field. Once we find the magnitude of the electric field we can use the equation

[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r_{mag}^2} }[/math]

to find the rmag value. To find [math]\displaystyle{ \hat r }[/math] we can find the direction of the electric field as that is obviously going to be in the same direction as [math]\displaystyle{ \hat r }[/math]. Then, once we find [math]\displaystyle{ \hat r }[/math], all that is left to do is multiply [math]\displaystyle{ \hat r }[/math] by rmag and that will give us the [math]\displaystyle{ r }[/math] vector. We can then find the location of the particle as we know [math]\displaystyle{ r=r_{observation}-r_{particle} }[/math]

Step 1: Find the magnitude of the Electric field.

[math]\displaystyle{ E }[/math]= (5.5*10^3, -7.6*10^3, 0) N/C

[math]\displaystyle{ E_{mag} }[/math] = [math]\displaystyle{ \sqrt{(5.5*10^3)^2+(-7.6*10^3)^2+0^2}=\sqrt{.8.8*10^7}= 9381 }[/math]

Step 2:: Rearrange the equation for the magnitude of electric field and solve for rmag.

[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r_{mag}^2} }[/math]

[math]\displaystyle{ r_{mag}^2= \frac{1}{4 \pi \epsilon_0 } \frac{q}{ E_{mag}} }[/math]

[math]\displaystyle{ r_{mag}^2= \frac{1}{4 \pi \epsilon_0 } \frac{2nC}{ 9381} }[/math]

[math]\displaystyle{ r_{mag}^2= .00192 }[/math]

[math]\displaystyle{ r_{mag}= .04m }[/math]

Step 3: Find the direction of the electric field

Because the source charge is negative, [math]\displaystyle{ \hat r }[/math] [math]\displaystyle{ =-\hat E }[/math]

[math]\displaystyle{ \hat E }[/math] [math]\displaystyle{ = E/ E_{mag} }[/math]

[math]\displaystyle{ \hat E }[/math] [math]\displaystyle{ = (\lt 5.5*10^3, -7.6*10^3, 0\gt / 9381) N/C }[/math]

[math]\displaystyle{ \hat r }[/math] [math]\displaystyle{ =-\hat E }[/math] = <-.56, .81,0>

Step 4: Find [math]\displaystyle{ r }[/math]

[math]\displaystyle{ r }[/math] = [math]\displaystyle{ r_{mag} }[/math] *[math]\displaystyle{ \hat r }[/math]

[math]\displaystyle{ r }[/math] = [math]\displaystyle{ .04m * \lt -.56, .81,0\gt }[/math]

[math]\displaystyle{ r }[/math] = [math]\displaystyle{ \lt -.02, .03, 0\gt m }[/math]

Step 5: Find [math]\displaystyle{ r_{particle} }[/math]

[math]\displaystyle{ r }[/math] [math]\displaystyle{ = r_{observation}- }[/math] [math]\displaystyle{ r_{particle} }[/math]

[math]\displaystyle{ r_{particle} }[/math] [math]\displaystyle{ = r_{observation}- }[/math] [math]\displaystyle{ r }[/math]

[math]\displaystyle{ r_{particle} }[/math] [math]\displaystyle{ = \lt .5.4, -1.8, 7.2\gt - }[/math] [math]\displaystyle{ \lt -.02, .03, 0\gt }[/math]

[math]\displaystyle{ r_{particle} }[/math] [math]\displaystyle{ =\lt 5.42, -1.83, 0\gt }[/math]

Connectedness

1.How is this topic connected to something that you are interested in?

I am really interested in the electric field of a point particle because it seems as if this one fundamental idea has so connections and relations throughout physics 2. Understanding this basic principle has helped me learn about much harder topics in magnetism.

2.How is it connected to your major?

I am a BME major and this is related to me because there are several instances where I will have to work with electric fields and circuits and this will be the foundation of what I do/learn.

3.Is there an interesting industrial application?

An interesting application is that electric fields of point charges can be used to find forces, both electric and magnetic forces. Then you can predict the motion of various particles looking at the forces that are acting upon them. .

History

Charles de Coulomb

Charles de Coulomb was born in June 14, 1736 in central France. He spent much of his early life in the military and was placed in regions throughout the world. He only began to do scientific experiments out of curiously on his military expeditions. However, when controversy arrived with him and the French bureaucracy coupled with the French Revolution, Coulomb had to leave France and thus really began his scientific career.

Between 1785 and 1791, de Coulomb wrote several key papers centered around multiple relations of electricity and magnetism. This helped him develop the principle known as Coulomb's Law, which confirmed that the force between two electrical charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. This is the same relationship that is seen in the electric field equation of a point charge.

Retrieved November 28, 2016, from http://www.biography.com/people/charles-de-coulomb-9259075#controversy-and-absolution

Point Charge

Contents

The Main Idea

A Mathematical Model of Electric Field due to Point Charge

A Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu