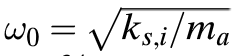Entropy

From Physics Book
Revision as of 21:01, 18 April 2018 by Nmoorman3 (talk | contribs)
Jump to navigation Jump to search 
Nina Moorman, Spring 2018

The Main Idea

Entropy is an important idea as it is crucial to both the fields of physics and chemistry, but often times it is hard to understand. The traditional definition of entropy is "the degree of disorder or randomness in the system" (Merriam). This definition can however can get lost on some people. A good way to visualize how entropy works is to think of it as a probability distribution with energy. In a sample space which includes two models and 8 quanta, you can configure each quanta to any system you like. All 8 quanta could go to one system, or they can be evenly distributed. If there each systems have equal probabilities of quanta levels, then a whole distribution can be formed around it. In this model, the probability that the energy will reach equilibrium is the highest, while scenarios where all the quanta is located in exclusively one of the two models have the lowest probability. In this way the new definition of entropy becomes "the direct measure of each energy configuration's probability." (Ted Talk)

A Mathematical Model

The goal of these formulas is to be able to calculate heat and temperature of certain objects:

Here is the formula to calculate Einstein's model of a solid:

Here is a formula to calculate how many ways there are to arrange q quanta among n one-dimensional oscillators:


From this you can directly calculate Entropy (S):

Where (The Boltzmann constant) Kb = 1.38 e -23

For a link to an image from NASA's website describing the entropy of a gas and the derivation of the specific form of the equation describing entropy found from manipulating the second law of thermodynamics, click the following link:

A Computational Model

How to calculate entropy with given n and q values:

https://trinket.io/embed/glowscript/c24ad7936e

Examples

Given the interatomic spring stiffness of copper is 28 N/m, answer the following:

Simple

For a nanoparticle consisting of 7 copper atoms, how many joules are there in the cluster of nano-particles?

Middling

What is the values of omega for 4 quanta of energy in the nano-particle?

Difficult

Calculate the entropy of the system given the answer from the previously calculated omega.

Connectedness

In my research I read that entropy is known as time's arrow, which in my opinion is one of the most powerful denotations of a physics term. Entropy is a fundamental law that makes the universe tick and it is such a powerful force that it will (possibly) cause the eventual end of the entire universe. Since entropy is always increases, over the expanse of an obscene amount of time the universe due to entropy will eventually suffer a "heat death" and cease to exist entirely. This is merely a scientific hypothesis, and though it may be gloom, an Asimov supercomputer Multivac may finally solve the Last Question and reboot the entire universe again.

The study of entropy is pertinent to my major as an Industrial Engineer as the whole idea of entropy is statistical thermodynamics. This is very similar to Industrial Engineering as it is essentially a statistical business major. Though the odds are unlikely that entropy will be directly used in the day of the life of an Industrial Engineer, the same distributions and concepts of probability are universal and carry over regardless of whether the example is of thermodynamic or business.

My understanding of quantum computers is no more than a couple of wikipedia articles and youtube videos, but I assume anything along the fields of quantum mechanics, which definitely relates to entropy, is important in making the chips to withstand intense heat transfers, etc.

History

The first person to give entropy a name was Rudolf Clausius. He questioned in his work the amount of usable heat lost during a reaction, and contrasted the previous view held by Sir Isaac Newton that heat was a physical particle. Clausius picked the name entropy as in Greek en + tropē means "transformation content."

The concept of Entropy was then expanded on by mainly Ludwig Boltzmann who essentially modeled entropy as a system of probability. Boltzmann gave a larger scale visualization method of an ideal gas in a container; he then stated that the logarithm of each of the micro-states each gas particle could inhabit times the constant he found was the definition of Entropy.

In this way Entropy came from an idea expounding terms of thermodynamics to a statistical thermodynamics which has many formulas and ways of calculation.

Regarding the relationship between entropy and the laws of thermodynamics, the second law of thermodynamics implies that the only processes that occur naturally while satisfying the first law of thermodynamics are those that do not decrease entropy (in other words those that increase or keep entropy the same). There is therefore no physical process that decreases the (universal) entropy.

See also

Here are a list of great resources about entropy that make it easier to understand, and also help expound more on the details of the topic.

Further reading

External links

Great TED-ED on the subject:

References

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Entropy&oldid=31930"