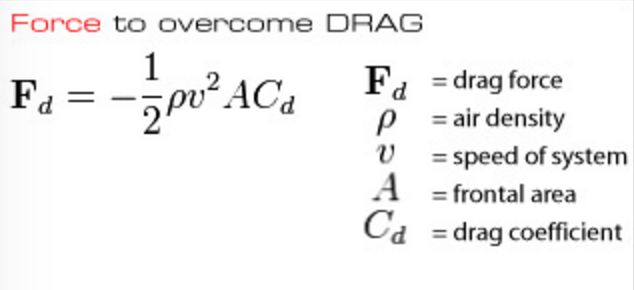Air Resistance
This page was completed by Jayanth Chintham (jchintham3). 11/29/15 THIS PAGE IS GOING TO BE EDITED by Cliff Panos (part of the Spring 2017 semester) This page is edited by Yuming Gao(10/29/18)
Introduction
The forces acting opposite to the direction of motion are called air resistance. Another term for this restraining effect is called "drag." Air resistance is a way of energy dissipation.

You may notice that when throwing a piece of tissue in the air, it floats slowly to the ground---this is the effect of air resistance. The force exerted by the air is pointing to the opposite direction of the object's motion. As you may have noticed in you daily life, air resistance is positively related to the speed of the object: when you hold an umbrella horizontally, pointing to the front, it is easier for you to walk slowly; but when you try to start running, you will notice the increasing force of air resistance is pushing you back. Another factor that impacts air resistance is the cross sectional area of a system. An example is a skydiver with an open parachute has more air resistance than a closed parachute. The last factor influencing air resistance is the density of air. An example is at higher altitudes (less air density) an object experiences weaker air resistance force.
The General Formula
The four factors that impact air resistance are cross sectional area, shape, air density, and speed. these four factors are included in the formula for the air resistance.
Variables and constants
As you can see in the picture above, air resistance in positively correlated to the density of the air, the cross-sectional area of the object, the square of the velocity, and the coefficient of air resistance, or 'drag coefficient.'
Cross Sectional Area
Since you must have been familiarized with the other two factors, we are going to go through details about the cross sectional area and the drag coefficient only. We have encountered the term of 'cross-sectional area' in many cases: for example, when you need to calculate the flux of a liquid through a pipe, you need the cross-sectional area to determine the volume of the liquid flowing through. However, the 'cross-sectional area' here is another story. We'd better see it as the 'frontal area': the area facing the direction of the object's movement.
It is easy to understand: we can relate this idea to the choice of the system and moving objects. For example, when a plane is flying forward with a speed v in the +x direction and the air is static, we are choosing the air as the system. But if we pick the plane as a system, the air as the moving object, it will have the same speed v in the -x direction. and only the surface of the plane pointing to the +x direction is subjected to the air resistance, since most air particles are colliding with that area with relatively high speed in the opposite direction.
Drag Coefficient
The drag coefficient is an identical number of the surrounding 'substrates' that engineers use to model all of the complex dependencies of shape and flow conditions on motion resistance(drag). It is usually determine by experiment since the factors are complex. The drag coefficient is a function of several parameters like shape of the body, Reynolds Number for the flow, Froude number, Mach Number and Roughness of the Surface. In short, different materials, substrates, and solvents have different drag coefficient.
A Computational Model
[Air Resistance Using Glowscript][1]
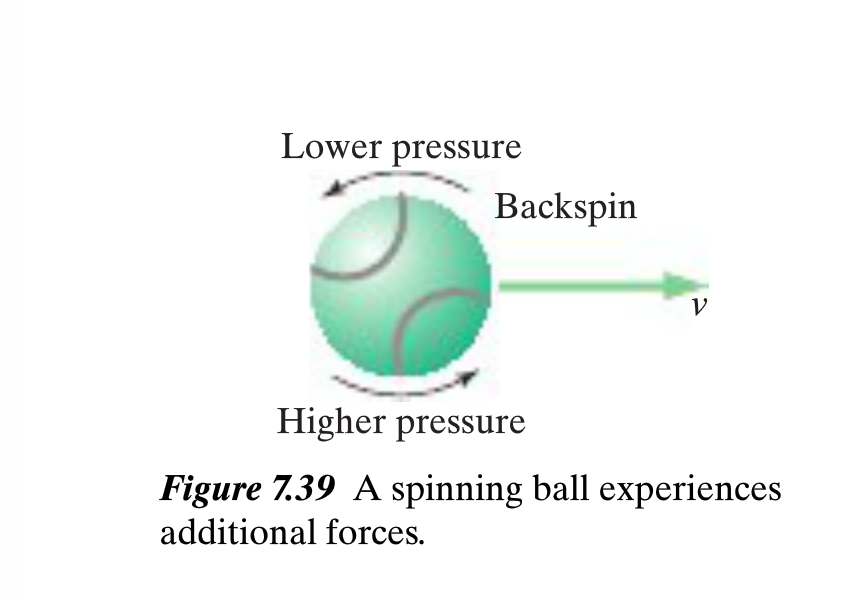
Rotational Motion on Air Resistance
If a ball has spin, there is an effect of fluid flow around the ball that raises the air pressure on the side where the rotational motion is in the same direction as the ball's velocity, and lowers the air pressure on the other side, where the rotational motion is in the opposite direction to the velocity. In the figure above, the force points upward due to "backspin" and lifts the ball extending the range. In the case where there is topspin on the ball, the force is downward decreasing the range. This topic is related to fluid dynamics.
Examples
Problem 1
You are standing at the top of a 20 building. You throw a ball in the horizontal direction with speed of 10 m/s. If you neglect air resistance, where would you expect the ball to hit on the plain surface below? Do you think your prediction without air resistance is too large or too small?
Solution:
height = (initial velocity in y direction)(time) + .5(acceleration from gravity)(time)^2
Since there is no initial velocity in the y direction, the equation is just:
height = .5(acceleration from gravity)(time)^2
20 = .5(9.8)(t)^2
Solve for t.
t = 2.02 seconds
range = (initial velocity in x direction)(time) + .5(acceleration in x direction)(time)^2
Since there is no acceleration in the x direction, the equation is just:
range = (initial velocity in x direction)(time)
range = (10)(2.02)
range = 20.2 meters
Our prediction without air resistance is too large, because air resistance has a force opposite to motion. This in turn would make the landing distance shorter.
Problem 2
John is going sky diving for the first time. His mass is 70 kg and his terminal speed is 38 m/s. What is the magnitude of the force of the air on John?
Solution:
At the terminal speed, the force of air (air resistance) is equal to the force of gravity.
Force air = Force gravity
Force air = (mass) (acceleration from gravity)
Force air = (70)(9.8)
Force air = 686 Newtons
Problem 3
Sarah is doing an air resistance experiment in class. The experiment requires Sarah to drop a coffee filter from a height of 2 meters. Let's say that the mass of the coffee filter was 2.0 grams, and it reached the ground with a speed of 1.0 m/s. How much kinetic energy did the air gain when Sarah dropped the coffee filter?
Solution:
Potential energy = (mass)(acceleration from gravity)(height)
Potential energy = (.002)(9.8)(2)
Potential energy = .0392 Joules
Kinetic Energy = .5(mass)(velocity)^2
Kinetic Energy = .5(.002)(1.0)^2
Kinetic Energy = .001 Joules
Total Energy = Potential Energy + Kinetic Energy
Total Energy = 0.0392 + 0.001 = 0.0402 Joules
Connectedness
How is this topic connected to something that you are interested in?
As an adventurous person, I have always been interested in skydiving. Air resistance is a huge factor in skydiving, as it allows you to reach the ground safely just with a parachute. There are many factors in releasing a parachute to have the safest possible landing. When you release your parachute and how to control your parachute are very important in having a safe landing. Also, there is obviously a lot of air resistance in a parachute because of the large cross sectional area.
Another topic that air resistance plays a factor in is sports. A specific sport that air resistance impacts is tennis. Spin is very important in tennis, because it allows you to control where the ball lands. If there is topspin on a ball, the air resistance is less allowing the ball to come down faster. If there is backspin, the ball stays in the air longer being controlled by the air.
How is it connected to your major?
I am an aerospace engineer, so air resistance has a lot of application in my field. Especially in aircraft design and manufacturing, aerospace engineers must design a aircraft that allows for the least air resistance. This allows for more control over the plane.
Is there an interesting industrial application?
Air resistance has a lot of application in speed sports. Also, air resistance plays a big factor in skydiving and anything with a parachute. Lastly, the aircraft industry factors in air resistance into all of their products, as this force is very important in certain situations.
History
Aristotle was the first to write about air resistance in the 4th century BC. In the 15th century, Leonardo da Vinci published the Codex Leicester, in which he rejected Aristotle's theory and attempted to prove that the only effect of air on a thrown object was to resist its motion. The first equation for air resistance was:
This equation overestimates drag in most cases, and was often used in the 19th century to argue the impossibility of human flight.
Louis Charles Breguet's paper of 1922 began efforts to reduce drag by streamlining. A further major call for streamlining was made by Sir Melvill Jones who provided the theoretical concepts to demonstrate emphatically the importance of streamlining in aircraft design. The aspect of Jones’s paper that most shocked the designers of the time was his plot of the horse power required versus velocity, for an actual and an ideal plane.
Further reading
http://www.physicsclassroom.com/class/newtlaws/Lesson-3/Free-Fall-and-Air-Resistance
http://www.forbes.com/sites/chadorzel/2015/09/29/the-annoying-physics-of-air-resistance/[2]
https://www.youtube.com/watch?v=mP1OTzdB0oI
References
Chabay, Ruth, and Bruce Sherwood. "Internal Energy." Matters and Interactions. 4th ed. Vol. 1. Wiley, 2015. Print.
More information can be found on drag[3] and aerodynamics[4]