Momentum Principle
This page discusses the Momentum Principle and examples of how it is used.
Claimed by Stephanie Oliva for Fall 2018
The Main Idea
In its most basic form, linear momentum is given by the product of mass and velocity. It is directly proportional to the magnitude of the mass and velocity of any particular object.
The Momentum Principle, also known as the Momentum Conservation Principle, states that for a collision occurring between object 1 and object 2 in an isolated system, the total momentum of the two objects before the collision equals their total momentum after the collision. This makes sense as it reiterates Newton's first law ( An object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force). When an external force affects the system, momentum can be changed. Overall, the momentum principle assumes that the final momentum is dependent on the initial momentum, the force applied, and the duration in which the force is applied. The product of force and time = impulse, the change in momentum.
History
The concept of momentum was first introduced by Descartes, a French scientist and philosopher before Newton. He invented the idea of mass and speed playing into the concept of “momentum”, meaning “amount of motion”. However, it soon came into discussion that the final motion could not be the same as initial. For example, if the mass of something increased or decreased (especially during inelastic collisions), momentum would have to change. At this time, Dutchman Christian Huygens pointed out that an object could have positive and negative momentum! Essentially, the direction that an object was traveling mattered (right would mean positive, and left would mean negative) and this would affect the motion of an object. This changed the definition of momentum to the product of mass and velocity instead, and upon further discussion, implied the idea of conserving momentum'. \
Newton's laws have also given us insight on what conservation of momentum means! By saying that the acceleration of a body and it's mass are related by force, and that all reactions have an equal and opposite reaction, conservation was deduced!
For more information, click here [1]!
Why the Momentum Principle Matters!
The Momentum Principle is a fundamental principle of mechanics and will prove highly relevant throughout your studies in Physics! It will be an important tool in our problem solving toolbox throughout the course. As our study of momentum progresses, it will also become apparent that our study of the Momentum Principle is very applicable to the everyday as well. You can consider the relation of momentum to the movement of objects in your life and the many industries that take advantage of the Momentum Principle to design products to fulfill certain purposes. This principle must also be considered in testing of these products.
For example, consider the role of the Momentum Principle plays in testing airbags and seat belts for cars. We might consider the final momentum of a car during an accident to be zero, assuming it comes to rest in the end. The initial momentum would be calculated based on the mass of the car and velocity at which it was initially moving. With the change in momentum fixed, the purpose of the airbag and seat belt becomes to increase the time taken for the body's momentum to reach zero (final momentum). This increase in time consequently reduces the force of the collision and protects the body from subsequent injury.
In sports, hitters are often encouraged to "follow-through" when striking a ball. If you follow through with your swing, the bat stays in contact with the ball for a longer period of time. It is generally true that greater time spent in contact with the ball causes the ball to go farther. We can consider the cause of such a phenomenon. It is not because of a greater force, this is a property dependent on the hitter! Instead, it is because increasing the time of the collision contributes to an increase in the velocity change of the ball! By following through, a hitter can hit the ball in such a way that it leaves the ball with more velocity (i.e., the ball is moving faster). In most sports, giving the ball a higher velocity often leads to greater success.
There are a great many more examples in our Universe where the Momentum Principle plays a vital role. Take, for another example, the movement of celestial bodies in our the solar system. If we consider the gravitational force acting between these bodies and the increase in velocity that ensues when these large bodies approach each other, we can see that momentum is always conserved!
In Industrial Engineering, a field largely concerned with improving efficiency and optimizing processes, the principle of linear momentum also plays a key role. Take, for example, the industrial engineer's task of maximizing the efficiency of a jet stream traveling through a curved pipe! Even though the speed of the stream might be consistent throughout the water's path, the curved shape of the pipe causes a change in momentum. This must be taken into consideration by the Industrial Engineer; who must, in turn, consider factors like the velocity at which the water is traveling, the width of the pipe, and the amount of water present etc.. in order to achieve the goal. Since IE tends to be based on improving pre-existing methods, it can be applied to almost any application of the momentum principle.
A Mathematical Model
The Momentum Principle is defined as [math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{system}= \vec{F}_{net} }[/math] (or [math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math]).
Alternatively, the momentum principle can be written as [math]\displaystyle{ \vec{p}_{f}=\vec{p}_{i}+\vec{F}_{net}* {∆t} }[/math].
[math]\displaystyle{ \vec{p} }[/math] is the momentum of the system. In the equation (and elsewhere), impulse (in [math]\displaystyle{ kg*{\frac{m}{s}} }[/math] ) is the "change in momentum" ([math]\displaystyle{ ∆\vec{p} = \vec{p}_{final} - \vec{p}_{initial} }[/math]), which includes both the magnitude and direction of the momentum. It is important to remember that momentum is a vector quantity.
[math]\displaystyle{ \vec{F}_{net} }[/math] is the net force from the surroundings. Force (measured in Newtons, or N) includes the interactions between the system and the surroundings, like the gravitational force exerted by the Earth on us or the force that a compressed spring exerts on a mass. Because momentum is defined as a vector; in the Momentum Principle, the force includes both the magnitude and direction. It is important to note that the Momentum Principle calls for the net force, which is the sum of all the different forces from the surroundings. This becomes essential when an object has multiple forces acting on it like the force of gravity, the force of a spring, force of friction, etc. as all of these, keeping in mind their respective directions, must ve added to obtain the net Force.
Solving Problems withe the Momentum Principle: Step by Step
Step 1: Define system and surroundings.
Step 2: Draw a free body diagram - This is a helpful way to determine the various forces acting on the system.
Step 3: Use the Momentum Principle to calculate the value needed.
Let's do an example!
In a crash test, a truck with mass 2200 kg traveling at 22 m/s smashes head-on into a concrete wall without rebounding. The front end crumples so much that the truck is 0.67 m shorter than before.
(a) What is the average speed of the truck during the collision (that is, during the interval between first contact with the wall and coming to a stop)?
Here, we use kinematic equations to solve for average velocity!
(b) About how long does the collision last? (That is, how long is the interval between first contact with the wall and coming to a stop?)
(c) What is the magnitude of the average force exerted by the wall on the truck during the collision?
Notice our 3 step procedure to solve, using the Momentum Principle! We have step 1- our system and surroundings, which helps with step 2- drawing a free body diagram! In our diagram, we can see that the force of the wall points to the left, which helps us then write it as a negative force in our equation (which makes sense, as we see our negative signs then cancel out each other!). We also notice our other forces, depicted by black arrows, but see that they will cancel each other out! Finally, we use our momentum principle in step 3- solving the equation!
A Computational Model
Click on the picture to read a description!
In this example, the ball is not moving, meaning it has a velocity of zero. If the velocity is zero, there is no change in momentum, meaning that net force is also zero. Therefore, we can conclude that initial and final momentum are equal due to the ball not moving. Therefore, [math]\displaystyle{ ∆\vec{p}=0 }[/math], and thus [math]\displaystyle{ \vec{F}_{net} = 0 }[/math]. Because the net force is equal to zero, this means that the force due to tension is equal in magnitude and opposite in direction to the force due to gravity.
[math]\displaystyle{ t }[/math] is the time (measured in seconds, or s). Specifically, the Momentum Principle calls for the "change in time" ([math]\displaystyle{ ∆\vec{t} = \vec{t}_{final} - \vec{t}_{initial} }[/math]), or in other words, the duration of the interaction is needed. Overall, if a force is applied to a system over a greater duration, the change in momentum is greater, as the momentum principle, [math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math], also demonstrates that the change in momentum is directly proportional to the duration of the applied force.
Momentum Principle Continued
The Momentum Principle can be further manipulated to find the change in velocity of the system. This is represented by the formula: [math]\displaystyle{ \vec{v}_{f}=\vec{v}_{i}+{\frac{\vec{F}_{net}}{m}}*{∆t} }[/math].
[math]\displaystyle{ \vec{v}_{f} }[/math] is the final velocity of the system, and [math]\displaystyle{ \vec{v}_{i} }[/math] is the initial velocity of the system. The difference between the two can be shortened to [math]\displaystyle{ \vec{{∆v}} }[/math], and represents the change in velocity of the system.
[math]\displaystyle{ \vec{F}_{net} }[/math] is the net force acting on the system.
[math]\displaystyle{ m }[/math] is the mass of the system.
[math]\displaystyle{ {∆t} }[/math] is the change in time of the system in which it is acted on by the force.
This manipulation of the momentum principle is very useful when it comes to updating the position of the system because it gives you the change in velocity over the observed time interval.
Previous Example Continued
Click on the link to see the Momentum Principle through VPython!
Make sure to press "Run" to see the principle in action!
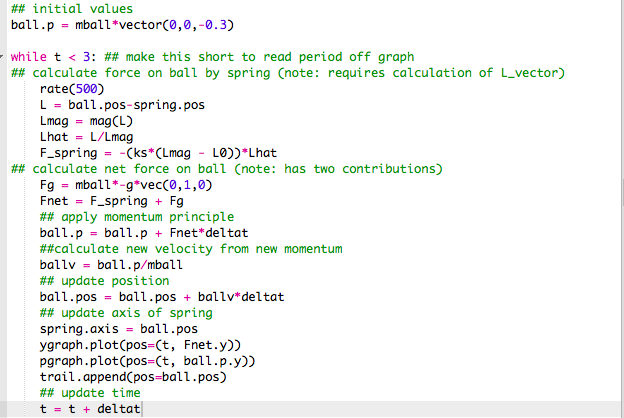
Here, we see the same ball and spring model from before, except we see the spring oscillating! This is because we start with a momentum (velocity greater than 0) and as the spring and ball move, we update net force. From each new net force, we have a new momentum. This new momentum gives us a new velocity, that we can then add to the ball's previous position to update its location.
This is depicted in this code:
We will now continue to add arrows depicting gravitational force, spring force, net force, and momentum to gain a better understanding of how each change as the Momentum Principle continues.
Net Force is depicted by the RED arrow. Gravitation Force is depicted by the BLUE arrow, like before. Spring Force is depicted by the WHITE arrow, like before. Momentum arrow is depicted by the ORANGE arrow.
The differences in the code now just allow for arrows to represent each value. You can see these changes here:
Let's Practice!
Simple
Two external forces <60,-70,0>N and <20,10,0>N, act on a system. What is the net force acting on the system?
Answer: <80,-60,0>N
Explanation:
The net force is just synonymous for the overall force acting on the system. In this case, this is the sum of the forces given in the problem above.
[math]\displaystyle{ \vec{F}_{net} = \vec{F}_{1} + \vec{F}_{2} }[/math]
[math]\displaystyle{ \vec{F}_{net} }[/math] = <60,-70,0)N + <20,10,0>N = <80,-60,0>N
Intermediate
A hockey puck is sliding along the ice with nearly constant momentum <16,0,5>kg*m/s when it is suddenly struck by a hockey stick with a force <0,0,2000>N that lasts for only 3 milliseconds (3e-3s). What is the new (vector) momentum of the puck?
Answer: <16,0,11>kg*m/s
Explanation:
In this example, we are manipulating the momentum principle in order to calculate the new momentum at a given time. This is also called the update momentum formula.
[math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math]
[math]\displaystyle{ \vec{p}_{final} - \vec{p}_{initial} }[/math] = [math]\displaystyle{ \vec{F}_{net} * {∆t} }[/math]
[math]\displaystyle{ \vec{p}_{final} }[/math] - <16,0,5>kg*m/s = <0,0,2000>N * (3e-3)s
[math]\displaystyle{ \vec{p}_{final} }[/math] = <16,0,11>kg*m/s
NOTE - Since there is no force in the x and y coordinates, momentum here remains constant.
Difficult
In outer space a rock of mass 5kg is acted on by a constant net force <29,-15,40>N during a 4s time interval. At the end of this time interval the rock has a velocity of <114,94,112>m/s. What is the rock's velocity at the beginning of the time interval?
Answer: <90.8,106,80>m/s
Explanation:
This example is similar to the first example. Only now, instead of manipulating variables to solve for momentum, we must manipulate the variables to solve for velocity, specifically initial velocity. Velocity can be connected to the momentum principle since momentum is just mass multiplied by velocity.
[math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math]
[math]\displaystyle{ \vec{p}_{final} - \vec{p}_{initial} = \vec{F}_{net} * {∆t} }[/math]
[math]\displaystyle{ \vec{p} = m * \vec{v} }[/math]
[math]\displaystyle{ m\vec{v}_{final} - m\vec{v}_{initial} = \vec{F}_{net} * {∆t} }[/math]
(5kg * <114,94,112>m/s) - (5kg * [math]\displaystyle{ \vec{v}_{initial} }[/math]) = <29,-15,40>N * 4s
[math]\displaystyle{ \vec{v}_{initial} }[/math] = <90.8,106,80>m/s
Further Reading
Read these to get some great further insight on this concept!
[1] http://acme.highpoint.edu/~atitus/phy221/lecture-notes/2-2-momentum-principle.pdf
[2] http://authors.library.caltech.edu/2577/1/TOLpr30c.pdf
As the Momentum Principle is the first of three fundamental principles of mechanics, the next possible topics to examine would be the other fundamental principles, the Energy Principle and the Angular Momentum Principle. Also, although the Momentum Principle is an extremely important concept that usually signals the start of a momentum related problem, the principal branches out into other momentum topics like Impulse and Iterative Prediction, which are used to solve other types of problems.
External links
[2] https://www.youtube.com/watch?v=ZvPrn3aBQG8
References
[1] William, Harris. "How Newton's Laws of Motion Work" 29 July 2008. HowStuffWorks.com. <https://science.howstuffworks.com/innovation/scientific-experiments/newton-law-of-motion.htm> 11 April, 2018.
[2] Sherwood, Bruce A. "2.1 The Momentum Principle." Matter & Interactions. By Ruth W. Chabay. 4th ed. Vol. 1. N.p.: John Wiley & Sons, 2015. 45-50. Print. Modern Mechanics. 8 April, 2018.
[3] Fenton, Flavio. "Momentum and Second Newton's Law." August-September Lectures. 2017.
[4] “Momentum Conservation Principle.” The Physics Classroom, <www.physicsclassroom.com/class/momentum/Lesson-2/Momentum-Conservation-Principle.> 13 April, 2018.
[5] Michael Fowler, U. Va. Physics. "Momentum, Work and Energy." Galileo and Einstein: Lecture Index. <http://galileoandeinstein.physics.virginia.edu/lectures/lecturelist.html>14 April, 2018.