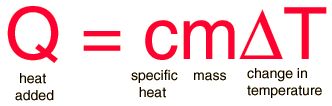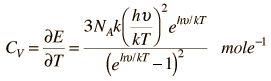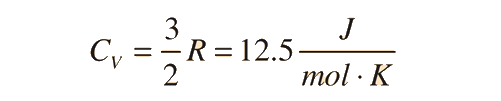Specific Heat

Main Idea

Mathematical Model

Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

The idea of Heat Capacity was first speculated by Albert Einstein is 1907 with his specific heat of solids lattice vibrations model, and later expanded by Peter Debye.

The Specific Heat of a substance, also known as the Specific Heat Capacity, is defined as the amount of energy required to raise the temperature of one gram of the substance by one degree Celsius. The units for specific heat are Joules per gram-degree Celsius (J / g °C). Specific heat is important as it can determine the thermal interaction a material has with other materials. We can test the validity of models with specific heat since it is experimentally measurable. The study of thermodynamics was sparked by the research done on specific heat. Thermodynamics is the study of the conversion of energy involving heat and temperature change of a system.

The Main Idea

The most common definition is that specific heat is the amount of heat needed to raise the temperature of 1 gram of a substance by 1 degree Celsius. The specific heat of a substance depends on its phase (solid, liquid, or gas) and its molecular structure. The relationship between heat and temperature change is best defined by the constant "c" in the equation below. Specific Heat is an intensive property, meaning that the amount of substance does not affect this property, only the composition of the subtance.

where:

m = the mass of the system (grams, g)

Q = the amount of heat added to the system, or change in thermal energy (Joules, J)

T = the temperature change (in Celsius ºC or Kelvin ºK)

c = the specific heat of the system ([Joules/(gram x degree celsius)], J/gºC)

The formula below is a reconfigured version of the relationship above. It shows how to calculate "c" specifically from the basic principle.

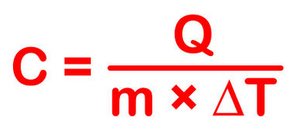
This equation does not apply if a phase change occurs (say from a liquid state to a gaseous state). This is because the amount of heat added or removed during a phase change does not change the overall temperature of the substance. So we disregard this relationship when phase changes take place.

The specific heat for solid can be calculated by the change in energy of the atoms over the change in temperature. The change in energy of the atoms is calculated by dividing the change in the energy of the system by the number of atoms in the substance.

The specific heat most commonly known is the specific heat for water, which is 4.186 J/g°C or 1 calorie/g°C. The specific heat of water is higher than any other common substance. Water has a very large specific heat on a per-gram basis, meaning that it takes a lot more added heat to cause a change in its temperature. Since the specific heat of water is so high, water can be used for temperature regulation. Due to the difference in atomic structures, the specific heat per gram of water is much higher than that of a metal substance. It is possible to predict the specific heat of any material, as long as you know about its atomic structure, as a rise in temperature is the increase in energy at the atomic level of substances. Generally, it is more more useful to compare molar specific heats of substances.

There are two models to determine the specific heats of substances at an atomic level. These are the Dulong-Petit Law and the Einstein-Debye model. The Dulong-Petit Law states that the molar specific heats of most solids (at room temperature or above) are almost constant. The Einstein-Debye model of specific heat states that specific heats drop at lower temperatures, as atomic processes become more relevant.

Here is an example of how to calculate specific heat.

Example: Find the specific heat of 350 g of an unknown substance when 34,700 Joules of heat are applied, and the temperature rises from 22ºC to 173ºC with no phase change.

We know that

m = 350 g

Q = 34,700 J

T initial = 22ºC

T final = 173ºC

c = ?

Using the formula above, c = Q / (mΔT)

c = 34,700 / (350*(173-22))

c = 34,700 / (350*151)

c = 34,700 / 52,850

c = 0.657 J/(gºC)

Common Specific Heats and Noticeable Trends

Air

Although with small temperature changes, the change in specific heat with temperature is ignored, it is worth noting that it does change with temperature as evident with air. The temperatures represented in the graph above are accessible. Specific heat typically decreases with a decrease in temperature and increases with an increase in temperature. Fun Fact: Specific heat approaches 0 near absolute zero. This is explained by the Debye model in a later section.

These are various specific heats of materials. Notice the difference of specific heat in the different phases of water.

http://physics.tutorcircle.com/heat/specific-heat.html

Using Specific Heat (Problem Solving)

More often, the specific heat of a substance can be looked up in a table or online, and it is unnecessary to find the specific heat. Instead, you will be asked to find the final temperature of a system. This can be done using the principle of the conservation of Energy

Example: Coffee at 93ºC with a specific heat of 4.2 J/gºC is mixed with 55.3 grams of creams at 5ºC (specific heat of 3.8). What is the final temperature?

The above solution was completed using the Principle of the Conservation of Energy. This principle states that the change of energy in a system should be equal to zero because energy cannot be created nor destroyed, which gives us the 0 on the right hand side of the equation. Assuming their is no heat transfer from the surroundings, this principle applies. For both substances, the masses are multiplied by the specific heats and the difference in temperature, and this is done to find their change in internal energy. Through the concept of convection we recognize that the substance with the higher temperature will lose energy, and this energy will be absorbed by the other substance, giving us a net energy change of 0. To convince yourself of this you can look at the units, the mass multiplied by the specific heat multiplied by the change in temperature.

g * J/gºC * ºC = J

leaves us with the energy unit Joules. Since the net change must equal zero we recognize that the energy lost by one substance is gained by the other, and the final temperature of the combined substances can be found.

In all cases, the two objects at different temperatures will reach the same final temperature. This is Thermal Equilibrium.

Suppose due to friction, a mule needed to do 40,000 J of work to power a 100 Watt bulb for 1 hour. The mill was cooled by 1 kg of water which starts at 4°C. What is the final temperature of the water (specific heat of water is 4.2 J/gK)?

First, we need to set up the problem symbolically.

Power=m_water C(T_f-T_(i,water) )

Next, we need to make sure our values have the correct units. Since the units for the specific heat are Joules/gram*Kelvin, we know that the unit of mass must be changed from kilograms to grams and the unit of temperature must be changed from Celsius to Kelvin.

m = 1kg *(1000g/1kg) = 1000g

T = 4°C + 273 = 277K

Now, we can plug these values into the equation.

40,000J=(1000g)(4.2 J/gK)(T_f-277K)

Now solve for the final temperature (Tf).

40,000J/(1000g)(4.2 J/gK) =T_f-277K

9.524K=T_f-277K

T_f= 286.52K

Lastly, we convert our answer back to Celsius.

Tf = 286.52K – 273 = 13.52°C

Therefore, the final temperature of the water will be 13.52°C.

Now let’s make things a little more complicated. We are going to go through an example that involves two different substances with different heat capacities and what happens to their temperatures when they come in contact.

A hot chunk of iron weighing 1.5 kg is placed into 2.5 kg of water at 14°C. The iron is at 250°C, and the heat capacity of iron is 0.45 J/gK. What is the final water temperature?

Notice: Although, the iron and water both have different values for mass (m), heat capacity (C), and initial temperature (Ti), they will both have the same final temperature. This is because the temperatures will continue to change as long as they are both different, but at the end of the reaction, the temperatures will have reached equilibrium.

Again, we will set up our problem symbolically.

m_water C_water (T_f-T_(i,water) )=m_iron C_iron (T_f-T_(i,iron) )

Since we are trying to find the final temperature, let’s solve the symbolic equation for that value before we plug in the numbers.

(m_water C_water+m_iron C_iron ) T_f=m_water C_water T_(i,water)-m_iron C_iron T_(i,iron)

T_f=(m_water C_water T_(i,water)-m_iron C_iron T_(i,iron))/(m_water C_water+m_iron C_iron )

Now, let’s write out the values for each of the variables and make sure they are in the correct units.

mwater = 2.5 kg * (1000g/1kg) = 2500g

Cwater = 4.2 J/gK

Ti,water = 14°C + 273 = 287 K

miron = 1.5 kg * (1000g/1kg) = 1500g

Ciron = 0.45 J/gK

Ti,iron = 250°C + 273 = 523 K

We can now plug these values in and solve for the final temperature.

T_f=((2500g)(4.2 J/gK)(287K)-(1500g)(0.45 J/gK)(523K))/((2500g)(4.2 J/gK)+(1500g)(0.45 J/gK) )

T_f=2660475/11175

T_f=238.07 K

Therefore, the final answer to this problem is 238.07 K.

Law of Dulong and Petit

The Law of Dulong and Petit is a thermodynamic law discovered in 1819 by the French physicists Pierre Louis Dulong and Alexis Thérèse Petit. It yields the expression for the molar specific heat capacity of certain chemical elements. They found, through experiments, that the mass specific heat capacity for many elements was close to a constant value, after it had been adjusted to reflect the relative atomic weight of the element.

Basically, Dulong and Petit found that the heat capacity of a mole of numerous solid elements is about 3R, where R is the universal gas constant. Dulong and Petit were unaware of the relationship to R, since it had not yet been defined. The value of 3R is about 25 joules per kelvin, and Dulong and Petit found that this was the approximate heat capacity of some solid elements per mole of atoms they contained.

Example The specific heat of copper is 0.389 J/gm K. The specific heat of lead is 0.128 J/gm K. Why are the values so different in these two metals? Did you notice that they are expressed as energy per unit mass? If you express each as energy per mole, they are actually very similar. The Law of Dulong and Petit addresses this similarity in molar specific heats. It can be accounted for by applying equipartition of energy to the atoms of solids.

When observed on a molar basis, the specific heats of copper and lead are as follows:

Copper: 0.386 J/gm K * 63.6 gm/mol = 24.6 J/mol K

Lead: 0.128 J/gm K * 207 gm/mol = 26.5 J/mol K

Other molar specific heats of metals are shown below:

Aluminum: 24.3 J/mol K

Gold: 25.6 J/mol K

Silver: 24.9 J/mol K

Zinc: 25.2 J/mol K

As you can see, molar specific heats of many metals are around 25 J/mol K and are really very similar.

Einstein Debye Model

Einstein and Debye had developed models for specific heat separately. Einstein's model stated that low energy excitation of a solid material was caused by oscillation of a single atom, whereas Debye's model stated that phonons or collective modes iterating through a material caused excitations. However, these two models are able to be put together to find the specific heat given by the following formula.

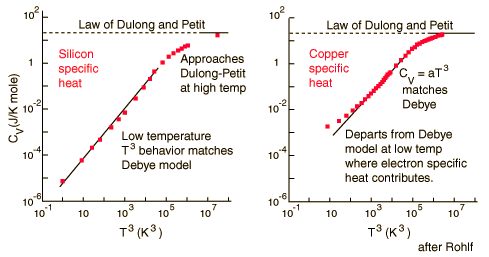
For low temperatures, Einstein and Debye found that the Law of Dulong and Petit was not applicable. At lower temperatures, it was found that atomic interactions were deemed significant in calculating the molar specific heat of an object.

According to the Einstein Debye Model for Copper and Aluminum, specific heat varies a lot at lower temperatures and goes much below the Dulong-Petit Model. This is due to increased effects on specific heat by interatomic forces. However, for very high temperatures, the Einstein-Debye Model cannot be used. In fact, at high temperatures, Einstein's expression of specific heat reduces to the Dulong-Petit mathematical expression.

The Einstein Debye Equation is below.

For high temperatures it may be reduced like this:

This actually reduces to the Dulong-Petit Formula for Specific Heat:

Specific Heats of Gases

The specific heats of gases are usually expressed as molar specific heats. For an ideal gas, the internal energy is all in the form of kinetic energy. The expression for the internal energy is

There are two specific heats for gases, one for gases at a constant volume and one gases at a constant pressure. In the formula below, the gas has a constant volume:

where Q is heat, n is number of moles, and delta T is change in Temperature.

For an ideal monatomic gas, the molar specific heat should be around:

For a constant pressure, specific heat can be derived as:

where Q is heat, n is number of moles, and delta T is change in Temperature.

For and ideal monatomic gas, the molar specific heat should be around:

The molar specific heats of gases all gravitate towards these ranges depending on the conditions the gas is kept in.

Specific Heat in Thermodynamics

While working on thermodynamic processes specific heat is differentiated between specific heat at a constant temperate <Cp> and specific heat at a constant volume <Cv>. For the scope of Physics 2211 it is not necessary to note this distinction. However, <Cp> and <Cv> can be indicative to the value of the other because

<Cp> = <Cv> + R

where R is the gas constant.

While dealing with in Thermodynamic processes it is also important to recognize that <Cp> values change through out different temperature ranges. To account for this the follow equation is utilized:

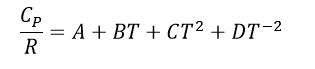
Where R is the gas constant, and A, B, C, and D are the heat capacity constants for the specific substance of interest which can be found in the back of thermodynamic textbooks or online.

Example of Heat Capacities Table

You may notice is in the particular table there are no D values listed. That is because D values are equal to 0 for gases, and C values are equal to 0 in liquids and solids.

It is easiest to find the Cp value by plugging in the constants into a program.

If working with vPython or glowscript you would simply have to write down the constants. Below is an example of what the program may look like.

The units which you should use for your temperature will be specified in your table where you get you A, B, C, and D values. From the table you will also note the units to determine which gas constant R is appropriate for the equation.

Connectedness

Specific heat and thermodynamics are used often in chemistry, nuclear engineering, aerodynamics, and mechanical engineering. It is also used in everyday life in the radiator and cooling system of a car.

Specific heat can have a lot to do with prosthetic manufacturing, which is a focus in Biomedical Engineering. Prosthetics materials must be durable and easy to manipulate in a normal range of temperatures. In order to created medical devices, specific heats must be known, especially for welding or molding things, which require a specific temperature to be effective. At higher temperatures, the Dulong-Petit law must be used to calculate the specific heat of an object. Especially for solid metal objects, which would be used in prosthetics, Dulong-Petit is very useful.

Cooking materials such as pots and pans are made to have a low specific heat so that they need less heat to raise their temperature. This allows for faster cooking processes. The handles of these cooking utensils are made of substances with high specific heats so that their temperature won’t rise too much if a large amount of heat is absorbed.

Have you ever noticed that sand on the beach can burn your feet but the ocean water is cool and refreshing? Sand has a lower specific heat than ocean water. So when the sun is beating down, the temperature of the land increases faster than that of the sea.

Insulation is made of materials with high specific heat so that they won't change temperature easily. For example, wood has a high specific heat. A wooden house helps keep the inside cooler during summer because it requires lots of heat to change its temperature. Builders can choose certain materials which allows us to build houses for specific locations and altitudes.