Translational, Rotational and Vibrational Energy

From Physics Book
Jump to navigation Jump to search

Main Idea

In many cases, analyzing the kinetic energy of an object is in fact more difficult than just applying the formula [math]\displaystyle{ K = \cfrac{1}{2}mv^2 }[/math]. An example of this is when throwing a basketball because not only does it move through the air, but it is also rotating around its own axis. When analyzing more complicated movements like this one, it is necessary to break kinetic energy into different parts, such as rotational, translational, and vibrational, and analyze each one separately to give a more accurate picture.

Translational kinetic energy is the kinetic energy associated with the motion of the center of mass of an object. This would be the basketball traveling in the air from one location to another. While relative kinetic energy is the kinetic energy associated to the rotation or vibration of the atoms of the object around its center or axis. Relative kinetic energy would be the rotation of the basketball around it's axis. Later on this page, we go into more depth about the different types of kinetic energy.

Here is a link to a video which explains kinetic energy in detail: [3]

Mathematical Model

Total Kinetic Energy

As we just saw, the total kinetic energy of a multi particle system can be divided into the energy associated with motion of the center of mass and the motion relative to the center of mass.

[math]\displaystyle{ K_{total} = K_{translational} + K_{relative} }[/math]

The relative kinetic energy is composed of motion due to rotation about the center of mass and vibrations/oscillations of the object.

[math]\displaystyle{ K_{total} = K_{translational} + K_{rotational} + K_{vibrational} }[/math]

Translational Kinetic Energy

"Translation" means:

To move from one location to another location

By calculating translational kinetic energy, we can track how one object moves from one location to another. Since the translational kinetic energy is associated with the movement of the center of mass of the object, it is important to know how to calculate the location of the center of mass and the velocity of the center of mass which is shown in the two equations below:

[math]\displaystyle{ r_{CM} = \cfrac{m_1r_1 + m_2r_2+m_3r_3 + ...}{m_1 + m_2 +m_3} }[/math]
[math]\displaystyle{ v_{CM} = \cfrac{m_1v_1 + m_2v_2+m_3v_3 + ...}{m_1+ m_2 +m_3} }[/math]
Here is a link to a video if you want to refresh your knowledge on center of mass: [4]

The motion of the center of mass is described by the velocity of the center of mass. Using the total mass and the velocity of the center of mass, we define the translational kinetic energy as:

[math]\displaystyle{ K_{translational} = \cfrac{1}{2}M_{total}v_{CM}^2 }[/math]

Vibrational Kinetic Energy

The total energy due to vibrations is the sum of the potential energy associated with interactions causing the vibrations and the kinetic energy of the vibrations.

[math]\displaystyle{ E_{vibrational} = K_{vibrational} + U_{s} }[/math]

The easiest way to find vibrational kinetic energy is by knowing the other energy terms and isolating the vibrational kinetic energy. This is when there is no rotational kinetic energy:

[math]\displaystyle{ E_{total} = K_{trans} + K_{vibrational} + U_{s} +E_{rest} }[/math]
[math]\displaystyle{ K_{vibrational} = E_{total} - (K_{trans} + U_{s} +E_{rest}) }[/math]

Rotational Kinetic Energy

Here are links to two videos that cover rotational kinetic energy and moment of interia: [1][2]

Rotational kinetic energy is the energy due to the rotation about the center of mass. It can be calculated by finding the angular momentum and inertia of the system, which will be discussed in greater detail in the next two sections. The equation used to find kinetic rotational energy is below:

[math]\displaystyle{ K_{rotational} =\frac{1}{2} I_{cm}{\omega}^2 }[/math]

Another important rotational equation is:

[math]\displaystyle{ }[/math]
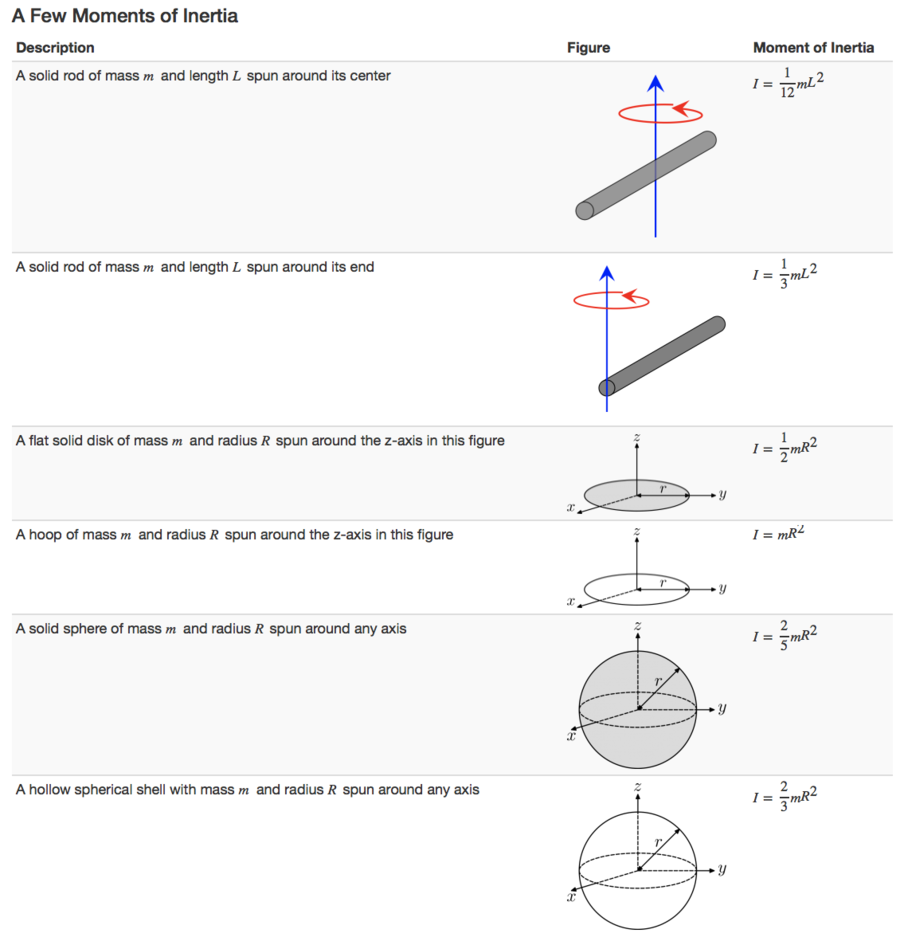
Moment of Inertia

The moment of inertia of an object shows the difficulty of rotating an object, since the larger the moment of inertia the more energy is required to rotate the object at the same angular velocity as an object with a smaller moment of inertia. The moment of inertia of an object is defined as the sum of the products of the mass of each particle in the object with the square of their distance from the axis of rotation. The general formula for calculating the moment of inertia of an object is:

[math]\displaystyle{ I = m_1{r_{1}}^2 + m_2{r_{2}}^2 + m_3{r_{3}}^2 +... }[/math]
Here [math]\displaystyle{ r_1, r_2, r_3 }[/math] represent the perpendicular distance from the point/axis of rotation.
or
[math]\displaystyle{ I = \sum_{i} m_{i}{r_{i}}^2 }[/math]
For a body with a uniform distribution of mass this can be turned into an integral:
[math]\displaystyle{ I = \int r^2 \ dm }[/math]

The units of rotational inertia are [math]\displaystyle{ kg \cdot m^2 }[/math]

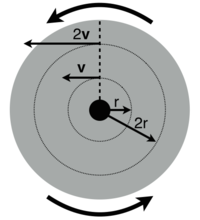
Angular Speed and Acceleration

The angular speed is the rate at which the object is rotating. It is given in the following formula:

[math]\displaystyle{ \omega = \cfrac{2\pi}{T} }[/math], where
[math]\displaystyle{ T = }[/math] the period of the rotation

The angle in which a disk turns is [math]\displaystyle{ 2 \pi }[/math] in a time [math]\displaystyle{ T }[/math]. It is measured in radians per second. The tangential velocity of an object is related to its radius r at the angular speed because the tangential velocity increases when the distance from the center of an object increases. It is shown in the equation below:

[math]\displaystyle{ v(r)= \omega r }[/math]

The angular acceleration a rotating object goes through to change its angular speed is given by:

[math]\displaystyle{ a(r) = \alpha r }[/math]

Computational Model

Insert Computational Model here

Examples

Simple

Middling

Difficult

Connectedness

1. How is this topic connected to something that you are interested in?

  • This topic connected to me because I used to dance when I was younger. This section focused on kinetic energy and the different parts of kinetic energy. You could break up different parts of dance and compare it to kinetic energy.

2. How is it connected to your major?

  • In Chemical Engineering, we will focus on the kinetic energy on the microscopic level and determining the energy of the particles by looking at the translational, rotational, and vibrational energies of the atom, and how they allow chemical reactions to precess.

3. Is there an interesting industrial application?

  • There are many machines that use kinetic energy for power, and we will probably see in a few years from now the use of rotational, translational, and vibrational energy to power anything from phones to computers.

History

Kinetic energy was first set apart from potential energy by Aristotle. Later, in the 1600's, Leibniz and Bernoulli developed the idea that [math]\displaystyle{ E \propto mv^2 }[/math], and they called it the 'living force.' However, it wasn't until 1829 that Gaspard-Gustave Coriolis showed the first signs of understanding kinetic energy the way that we do today by focusing on the transfer on energy in rotating water wheels. Finally, in 1849, Lord Kelvin is said to have coined the term 'kinetic energy.'

See also

Further Reading

External Links

References

All problem examples, youtube videos, and images are from the websites referenced below:

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Translational,_Rotational_and_Vibrational_Energy&oldid=37248"