Transformers (Circuits)
Electricity sent through power lines is transmitted with high voltages through long thick power lines because wires have a resistance that causes power loss at a rate proportional to the current squared. By transmitting at a high voltage, energy loss is minimized. Home appliances however operate at much lower voltages. Something is needed to convert the power to a high current, low voltage power that home appliances can use. This conversion from high voltage to low voltage, and vice versa, is accomplished by a transformer.
Background
Inductance
Currents can be induced (produced) by changing the current through a coil. This is due to the changing magnetic field [math]\displaystyle{ \textstyle (dB/dt) }[/math] produced by varying the current through the coil. We know from the Maxwell-Faraday Law of Maxwell's Equations:
[math]\displaystyle{ |emf| = \oint \overrightarrow{E}_{NC} \cdot d\overrightarrow{l} = \left | \frac{d\phi_{mag}}{dt} \right \vert }[/math]
Or that a changing magnetic field through an area produces a non-Coloumb electric field.
Mathematical Formulae
Before moving on to a discussion of the mathematics of transformers, here are some formulas it will be helpful to recall:
- Magnetic Field Inside a Solenoid: [math]\displaystyle{ B=\frac{\mu_0 N I}{d} }[/math]
- Where [math]\displaystyle{ \textstyle N }[/math] is the number of coils and [math]\displaystyle{ \textstyle d }[/math] is the length of the solenoid.
- Magnitude of self-induced emf: [math]\displaystyle{ \textstyle \left|emf_{ind}\right \vert=L\left|\frac{d I}{d t} \right \vert }[/math]
- Where [math]\displaystyle{ L }[/math] is the proportionality constant called the "inductance" or "self-inductance" which equals [math]\displaystyle{ \textstyle \frac{\mu_0 N^2}{d}\pi R^2 }[/math]
- Expanding this, we get the self-induced emf in a solenoid is: [math]\displaystyle{ \textstyle emf= \frac{\mu_0 N^2}{d}\pi R^2 \frac{d I}{d t} }[/math]
- Finally, remember your units. [math]\displaystyle{ emf }[/math] is measured in volts, self-inductance is [math]\displaystyle{ \textstyle(V•s/A) }[/math] or the "henry" (H), and [math]\displaystyle{ B }[/math] is measured in Tesla (T) or [math]\displaystyle{ \textstyle(\frac{kg}{s^2 A}) }[/math]
How They Work
Conversion from high to low, or low to high voltage can be accomplished using the principles discussed above. Consider a solenoid with [math]\displaystyle{ N_1=100 }[/math] coils around a hollow cylinder of length [math]\displaystyle{ d=.3 m }[/math]. Now wrap [math]\displaystyle{ N_2 = 200 }[/math] coils around this solenoid to form the secondary coil. If an alternating current is run through the primary coil, we get a non-zero [math]\displaystyle{ \textstyle\frac{d I}{d t} }[/math]We can now calculate the potential difference across each coil.
Primary Coil
As stated above, the induced emf in the primary coil is [math]\displaystyle{ L\left|\frac{d I}{d t} \right \vert }[/math]. Expanding this and substituting [math]\displaystyle{ A=\pi R^2 }[/math] for the area, we get a potential difference across the primary coil of [math]\displaystyle{ \textstyle A(\mu_0 N_1^2 /d)dI/dt }[/math].
Secondary Coil
A current is induced in the secondary coil by the changing magnetic field produced by the primary coil. The magnetic field is [math]\displaystyle{ \textstyle B = \mu_0 N_1 I/d }[/math] and it is changing across area [math]\displaystyle{ A }[/math] (which is only the area of the inner coil, not the outer secondary coil. So the emf in one turn of the secondary coil is [math]\displaystyle{ A dB/dt }[/math].
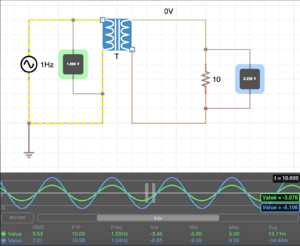
Circuits
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
See also
This will give you a general understanding of Faraday's Law, which is the basis behind transformer technology.
Inductance is another property of an electrical conductor derived from Faraday's law.
Changing the flux of a magnetic field around a coil will induce voltage.
Further reading
Books, Articles or other print media on this topic
External links
http://www.edisontechcenter.org/Transformers.html
References
Chabay, R., & Sherwood, B. (2015). Electric Potential. In Matter & interactions (4th ed., Vol. Two, pp. 920). Danvers, Massachusetts: J. Wiley & sons.