Pendulum Motion
--mbriatta3 (talk) 14:17, 3 December 2015 (EST)
The pendulum is a mass hanging from a string of negligible mass that is fixed to a point. The equilibrium position of the pendulum is the position when the string and mass hang vertically downward. When pulled back away from this equilibrium state, the string and mass will swing back and forth. If there is no friction or air resistance applied then the pendulum will swing forever.
The Main Idea
Properties of Pendulum Motion
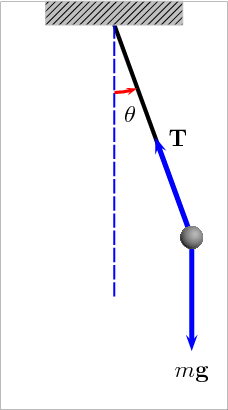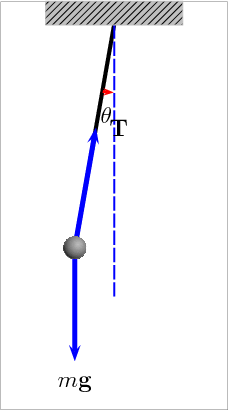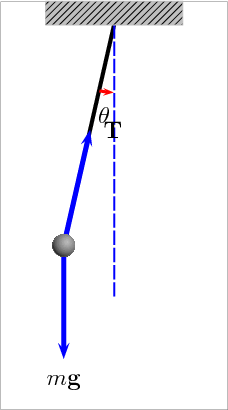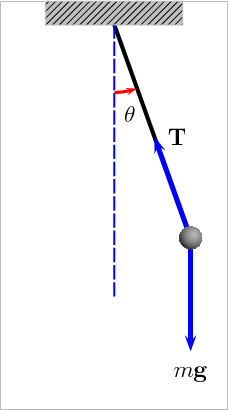
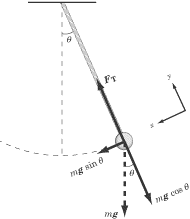
Animation of a pendulum showing forces acting on the mass: the tension T in the rod and the gravitational force mg. Link
A pendulum is just a mass hanging from a spring moving back and forth. In order to describe a pendulum, you need to understand its properties and parameters. There is a string with length L, a mass m hanging from the string, and it is pulled away from its equilibrium, there is an angle measured off the vertical. The two forces acting on the pendulum when it is pulled away from its equilibrium are the string tension, Ft and the gravity, F = mg.
Period of Oscillation
The period of oscillation of the pendulum, T, is defined in terms of the acceleration due to gravity, g, and the length of the pendulum, L, and to a small extent on the maximum angle that the pendulum swings away from vertical, θ0, called the amplitude
- [math]\displaystyle{ T \approx 2\pi \sqrt\frac{L}{g} \qquad \qquad \qquad \theta_0 \ll 1 \, }[/math]
This is a pretty scary-looking equation, but there’s really only one thing you need to gather from it: the longer the pendulum rope, the longer it will take for the pendulum to oscillate back and forth. You should also note that the mass of the pendulum bob and the angle of displacement play no role in determining the period of oscillation.
Energy
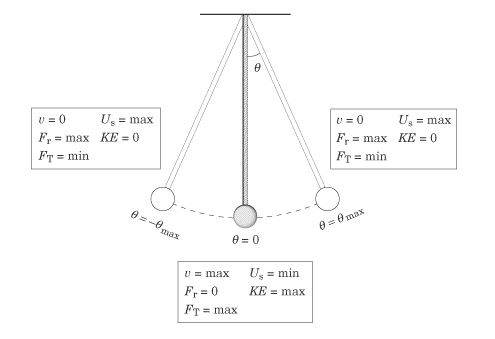
The mechanical energy of the pendulum is a conserved quantity. The potential energy of the pendulum, mgh, increases with the height of the bob; therefore the potential energy is minimized at the equilibrium point and is maximized at . Conversely, the kinetic energy and velocity of the pendulum are maximized at the equilibrium point and minimized when . The figure below summarizes this information in a qualitative manner, which is the manner in which you are most likely to find it on SAT II Physics. In this figure, v signifies velocity, signifies the restoring force, signifies the tension in the pendulum string, U signifies potential energy, and KE signifies kinetic energy.
Velocity

Calculating the velocity of the pendulum bob at the equilibrium position requires that we arrange our coordinate system so that the height of the bob at the equilibrium position is zero. Then the total mechanical energy is equal to the kinetic energy at the equilibrium point where U = 0. The total mechanical energy is also equal to the total potential energy at where KE = 0. Putting these equalities together, we get
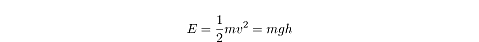
But what is h?
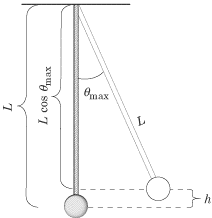
From the figure, we see that ![]() If we plug that value into the equation above, we can solve for v:
If we plug that value into the equation above, we can solve for v: 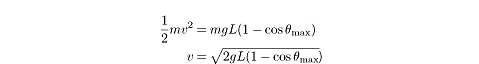
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
Middling
Difficult
Connectedness
Talk about clocks
As you see, the pendulum motion can be seen in our everyday life. As an architecture major, I have always been interested art and design. Different sculptures, installations, and art pieces can even be achieved throughout the application of a pendulum motion. Take a look here and here and here
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
- Barton's Pendulums
- Double Pendulum
- Pendulum Clock
- Pendulum (mathematics)
- Spherical Pendulum
- Simple Harmonic Motion
Further reading
- G. L. Baker and J. A. Blackburn (2009). The Pendulum: A Case Study in Physics (Oxford University Press).
- M. Gitterman (2010). The Chaotic Pendulum (World Scientific).
- Michael R. Matthews, Arthur Stinner, Colin F. Gauld (2005)The Pendulum: Scientific, Historical, Philosophical and Educational Perspectives, Springer
- Michael R. Matthews, Colin Gauld and Arthur Stinner (2005) The Pendulum: Its Place in Science, Culture and Pedagogy. Science & Education, 13, 261-277.
- Schlomo Silbermann,(2014) "Pendulum Fundamental; The Path Of Nowhere" (Book)
- Matthys, Robert J. (2004). Accurate Pendulum Clocks. UK: Oxford Univ. Press. ISBN 0-19-852971-6.
- Nelson, Robert; M. G. Olsson (February 1986). "The pendulum – Rich physics from a simple system". American Journal of Physics 54 (2): 112–121. Bibcode:1986AmJPh..54..112N. doi:10.1119/1.14703.
- L. P. Pook (2011). Understanding Pendulums: A Brief Introduction (Springer).
External links
References
- Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2011. Print.
- "Pendulum Motion." Pendulum Motion. Physics Classroom, 1996. Web. 03 Dec. 2015.
- "Pendulum." Wikipedia. Wikimedia Foundation, n.d. Web. 03 Dec. 2015.