Motional Emf using Faraday's Law

Claimed by Chelsea Calhoun

The Main Idea

When a wire moves through an area of magnetic field, a current begins to flow along the wire as a result of magnetic forces. Originally, we learned to calculate the motional emf in a moving bar by using the equation [math]\displaystyle{ {\frac{q(\vec{v} \times \vec{B})L}{q}} }[/math]. However, there's an easier way to do this: by writing an equation for emf in terms of magnetic flux.

A Mathematical Model

We know that the magnitude of motional emf is equal to the rate of change of magnetic flux. [math]\displaystyle{ |emf| = \left|\frac{d\Phi_m}{dt}\right| }[/math]

We also know that magnetic flux is defined by the formula: [math]\displaystyle{ \Phi_m = \int\! \vec{B} \cdot\vec{n}dA }[/math]

When a metal bar or wire is moving across an area, creating a closed circuit, the magnetic field contained inside the area of the circuit is no longer constant. When there is a non-constant magnetic field, we must use Faraday's law (a combination of the two equations above) to solve for motional emf.

Faraday's Law is defined as: [math]\displaystyle{ emf = \int\! \vec{E} \cdot d\vec{l} = -\frac{d}{dt} \int\! \vec{B} \cdot \vec{n}dA }[/math]

where [math]\displaystyle{ \vec{E} }[/math] is the electric field along the path, [math]\displaystyle{ l }[/math] is the length of the path you're integrating on, [math]\displaystyle{ \vec{B} }[/math] is the magnetic field inside the area enclosed, and [math]\displaystyle{ \vec{n} }[/math] is the unit vector perpendicular to area A.

A Computational Model

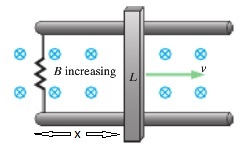
In the image shown above, a bar of length [math]\displaystyle{ L }[/math] is moving along two other bars from right to left. The blue circles containing "x"s represent a magnetic field directed into the page. As the bar moves to the right, the system encircles a greater amount of magnetic field. To explain this concept more clearly, take a look at the figures below. This image shows a bar moving in a magnetic field at two different times. In the first picture, at time [math]\displaystyle{ t_1 }[/math], the system encircles half of two individual magnetic field circles. However, in the second picture taken at time [math]\displaystyle{ t_2 }[/math], the system now encircles 6 full magnetic field circles. Of course, this explanation isn't using technical terms, but the point still stands: the magnetic field is increasing as time increases.

Returning to the scenario in the first image, because the magnetic field is not constant, we can use Faraday's Law to solve for the motional emf.

As stated above, the formula is as follows:

[math]\displaystyle{ emf = -\frac{d}{dt} \int\! \vec{B} \cdot \vec{n}dA }[/math]

First, integrate the integral with respect to the area of the rectangle enclosed.

[math]\displaystyle{ emf = -\frac{d}{dt} (\vec{B} \cdot \vec{n}A) }[/math]

We have the dimensions of the bar in variables: length [math]\displaystyle{ L }[/math] and width [math]\displaystyle{ x }[/math]. Substitute these values for the area, [math]\displaystyle{ A }[/math]

[math]\displaystyle{ emf = -\frac{d}{dt} (\vec{B} \cdot \vec{n}(L)(x)) }[/math]

Now that we have this formula, we have to figure out how to take its derivative with respect to [math]\displaystyle{ t }[/math]. Which of the magnitudes of these values is changing?

The magnitude of the magnetic field is constant. (More "circles" are added as time increases, but the magnitude of each "circle" does not change.

The magnitude of the normal vector is constant.

The length, [math]\displaystyle{ L }[/math], of the bar is constant.

The width of the surface enclosed, [math]\displaystyle{ x }[/math], changes.

As a result, the formula now becomes:

[math]\displaystyle{ emf = (\vec{B} \cdot \vec{n}(L))\left(-\frac{d}{dt}(x)\right) }[/math]

In this case, [math]\displaystyle{ \frac{dx}{dt} = \vec{v} }[/math] because [math]\displaystyle{ x }[/math] is a function of time, where [math]\displaystyle{ \vec{v} }[/math] is the velocity of the moving bar. Substituting that in, we get:

[math]\displaystyle{ emf = (\vec{B} \cdot \vec{n}(L))\vec{v} }[/math]

Plugging in these values, we can solve for the motional emf of the bar.

Because the magnetic field is changing with time, however, there is also an induced current flowing through the circuit. We can find the direction of the current using the right hand rule. To do this, we can use 2 different methods:

1. We can use the equation [math]\displaystyle{ \vec{F} = q\vec{v} \times \vec{B} }[/math], where [math]\displaystyle{ \vec{F} }[/math] is the force on the bar, and [math]\displaystyle{ \vec{v} }[/math] is the velocity of the bar. Using the right hand rule, we can point our fingers in the direction of the velocity of the bar and curl them in the direction of the magnetic field. The direction that our thumb points is the direction of the force on a positive charge. In this case, [math]\displaystyle{ \vec{F} }[/math] points upward, so the positive charges in the bar will move to the top, causing it to polarize with positive charges at the top and negative charges at the bottom. We can now visualize the bar as a battery that causes a current [math]\displaystyle{ I }[/math] to run out of the positive end. In this case, since the bar is polarized with the positive charges at the top, the current will flow out of the top of the bar and continue around the circuit.

2. We can use the negative direction of the change in magnetic field, [math]\displaystyle{ -\frac{dB}{dt} }[/math] to find the direction of the current. To do this, make a diagram comparing the magnitude of the magnetic field enclosed at time [math]\displaystyle{ t_1 }[/math] and at time [math]\displaystyle{ t_2 }[/math]. Then, draw an arrow representing the direction of change of the magnetic field. Now, flip the arrow to take the negative of that vector's direction. Using the right hand rule, point your thumb in the direction of [math]\displaystyle{ -\frac{dB}{dt} }[/math], and the curl of your fingers will give you the direction of the induced current, [math]\displaystyle{ I }[/math].

If the magnetic field is NOT constant, meaning it changes with time, the derivative [math]\displaystyle{ \frac{d}{dt} }[/math] will be distributed to both [math]\displaystyle{ \vec{B} }[/math] and [math]\displaystyle{ x }[/math] in the formula. In this case, we must use the product rule to be able to set up the equation and continue solving for [math]\displaystyle{ emf }[/math].

[math]\displaystyle{ emf = -(\frac{d}{dt} \vec{B})A \cdot B(\frac{d}{dt}A) }[/math]

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

Using the figure below, identify the following.

a) Direction of magnetic field

b) Direction of change in magnetic field, [math]\displaystyle{ \frac{d\vec{B}}{dt} }[/math]

c) Direction of negative change in magnetic field, [math]\displaystyle{ -\frac{d\vec{B}}{dt} }[/math]

d) Direction of current, [math]\displaystyle{ I }[/math]

e) Polarization of moving bar

f) Direction of electric field inside bar due to polarization

g) Direction of force on bar

SOLUTION:

a) Into the page

A circle with an 'x' inside of it represents a vector into the page. A circle with a dot inside represents a vector out of the page.

b) Into the page

Initially, at the time of the image, there are 4 circles representing magnetic field enclosed by the bars. However, as the bar moves, at some time t, the number of circles enclosed by the bar will increase; therefore, there is more magnetic field inside the loop. This means that the change in magnetic field is in the direction of the magnetic field.

c) Out of the page

The negative change in magnetic field is in the opposite direction as change in magnetic field.

d) Counterclockwise

Point your thumb in the direction of [math]\displaystyle{ -\frac{d\vec{B}}{dt} }[/math]. Your fingers will curl in the direction of current.

e) Positive charges at the top, negative charges at the bottom

The electric force on a particle is [math]\displaystyle{ \vec{F} = q\vec{v} \times \vec{B} }[/math], so point your fingers in the direction of the velocity of the bar and curl them in the direction of magnetic field. The direction of your thumb is the direction of force on a positive particle.

f) Down

Positive charges have an electric field that points away from them while negative particles have an electric field that point towards them. If the top of the bar is positively charged, the field will point downward toward the negative particles.

g) Left

When a current is involved, [math]\displaystyle{ \vec{F} = I\vec{l} \times \vec{B} }[/math], so point your fingers in the direction of the length of the bar (in the direction of current) and curl them in the direction of magnetic field. The direction of your thumb is the direction of force on the bar.

Medium

A bar of length [math]\displaystyle{ L = 2 }[/math] is moving across two other bars in a region of magnetic field, [math]\displaystyle{ B = 1.3E-3 }[/math] directed into the page. The bar is moving with a velocity of 10 m/s, and [math]\displaystyle{ x }[/math] is the width of the area enclosed. What is the magnitude of the [math]\displaystyle{ emf }[/math] produced?

SOLUTION:

Because the magnetic field enclosed by the system is changing with time, we must use Faraday's Law: [math]\displaystyle{ |emf| = \frac{d}{dt} \int\! \vec{B} \cdot \vec{n}dA }[/math]

First, integrate through the formula: [math]\displaystyle{ |emf| = \frac{d}{dt} \vec{B} \cdot A }[/math]

Area [math]\displaystyle{ A = Lx }[/math]

Next, distribute [math]\displaystyle{ \frac{d}{dt} }[/math]. In this case, distance [math]\displaystyle{ x }[/math] is what is changing, so the formula becomes: [math]\displaystyle{ |emf| = \vec{B} \cdot L\frac{d}{dt}x }[/math]

The derivative of distance is velocity. [math]\displaystyle{ \frac{dx}{dt} = v }[/math]

Therefore, |emf| in this problem is equal to [math]\displaystyle{ BLv = .026 V }[/math]

Difficult

A long straight wire carrying current [math]\displaystyle{ I = .3 A }[/math] is moving with speed [math]\displaystyle{ v = 5 m/s }[/math] toward a small circular coil of radius [math]\displaystyle{ R = .005 }[/math] and 10 turns. The long wire is in the plane of the coil. The coil is very small, so that, at any fixed moment in time, you can neglect the spatial variation of the wire's magnetic field over the area of the coil.

a) Is the induced current in the coil flowing clockwise or counterclockwise?

b) At the instant when the long wire is a distance [math]\displaystyle{ x = 4 m }[/math] from the center of the coil, determine the magnitude of the induced emf in the coil.

Now consider the case where the wire is stationary and the coil is moving down parallel to the wire with a constant speed, [math]\displaystyle{ v = 2 m/s }[/math].

c) At the instant when the long wire is a distance [math]\displaystyle{ x = 4 m }[/math] from the center of the coil, determine the magnitude of the induced emf in the coil.

SOLUTION:

a) Counterclockwise

Using the right hand rule, if you point your thumb in the direction of current (+y), your fingers will curl in the direction of magnetic field. In this case, magnetic field is pointing into the page at the coil. At the location of the coil, the magnitude of the magnetic field due to the wire is increasing as the wire moves closer; therefore, [math]\displaystyle{ \frac{d\vec{B}}{dt} }[/math] is pointing into the page, and [math]\displaystyle{ -\frac{d\vec{B}}{dt} }[/math] is pointing out of the page. If you point your thumb in the direction of [math]\displaystyle{ -\frac{d\vec{B}}{dt} }[/math], your fingers curl in the direction of the induced current.

b) [math]\displaystyle{ |emf| = 1.47E-11 V }[/math]

After integrating Faraday's Law, we get

Connectedness

1. How is this topic connected to something that you are interested in?

In physics 1, we focused on large scale, physical pieces of matter, kinetics and rotation, which I personally find fairly interesting. Physics 2, however, focuses on new, small-scale concepts that can often be more challenging to envision since topics like electric and magnetic fields are not something we can see with the naked eye. With motional emf, though, problems now become more visual, and many times can be conceptually solved using the right hand rule. It's interesting to learn about how something as simple as moving a bar through space filled with a magnetic field can cause a current to flow. A system like this could even potentially be used in the place of a battery.

2. How is it connected to your major?

I am currently majoring in mechanical engineering, and in this field, we are required to work with both mechanics and circuit-like scenarios. Personally, I am interested in going into the car manufacturing industry, where motional emf plays a very important role. When you move an object through a magnetic field, it resists movement and generates electricity in the loop. If this is done with enough force, it could be used to stop a small car or roller-coaster.

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

Motional Emf using Faraday's Law

Contents

The Main Idea

A Mathematical Model

A Computational Model

Examples

Simple

Medium

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu