Angular Velocity

CLAIMED By Josh Mathew

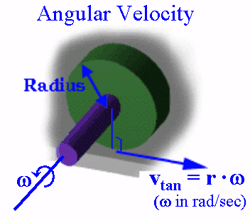
Angular Velocity describes the rate of change around a center of mass. It is measured in radians/second.

Angular Momentum also known as Rotational velocity

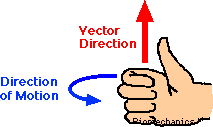
In order to find out the velocity of things which revolve around a body we have to take account not just speed but also the radius of which it is revolving around. The central angle in which objects rotate around is constantly changing, therefore that is why linear velocity is not adequate to measure the rate of change of the angle. Angular velocity is this rate of change with respect to time. In order to figure out the direction of angular velocity we can use the Right hand rule. It is important to note the definition of linear velocity, which is the rate of change of position measured in meters with respect to time. The only difference between the two is the fact that the object is rotating around something. The direction is perpendicular to the plane of the rotation. Often angular velocity is used to figure out rotational angular momentum and very useful when figuring out the speed of something rotating or orbiting around something.

A Mathematical Model

Angular Momentum of an object can be described as a the radius of the object of which it is rotating around its center of mass diveded by its linear velocity.

ω = dθ/dt

dθ= rate of change of the radians or degrees dt= rate of change of time throughout the interval

V perpendicular = mag(V)*sin(θ) V= linear velocity θ= Angle of which the linear velocity is going.

Thus after combining the two definitions we get

ω = R/v ω= The greek symbol of omega symbolizes angular velocity R= The radius of the body of which is rotates, measured in radians V= Linear Velocity

Also another we can compute angular velocity is if Angular Momentum is given. L = Iω L= Angular Momentum I = Moment of inertia ω = Angular Velocity

A Computational Model

Check out this code which gives an example of angular velocity. It is an example found http://vpython.org/contents/contributed/rotating_book.py

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

A circular wheel of 0.50 m radius is moving with a speed of 10 m/s. Find the angular velocity?

The angular velocity is given by ω = dθ/dt dθ= 10 dt= .5 = 20 rads/ sec

Middling

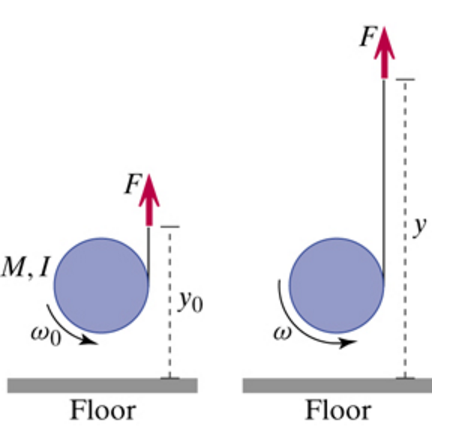
String is wrapped around an object of mass M = 0.3 kg and moment of inertia I = 0.01 kgÂ·m2. You pull the string with your hand straight up with some constant force F such that the center of the object does not move up or down, but the object spins faster and faster (see the figure). This is like a yo-yo; nothing but the vertical string touches the object. When your hand is a height y0 = 0.29 m above the floor, the object has an angular speed = 13 radians/s. When your hand has risen to a height y = 0.69 m above the floor, what is the angular speed of the object? Your answer must be numeric and not contain the symbol F.

To solve we must start from the fundamental energy principle. The only energy here is rotational kinetic energy. Work= Fnet*Distance = change in energy = change in rotational kinetic energy. F= MG = .3(9.8) Distance= Displacement of the hand. (.69-.29) .5IW^2(initial)= .5(.01)(13)^2 .5IW^2(final)= .5(.01)(?)^2

Plug and chug.

(.3)(9.8)(4) = .5(.01)(Wf?)^2 - .5(.01)(13)^2 Solve for Final Angular Velocity (Wf) Final answer= 20.1 radians/s

Difficult

A spherical satellite of approximately uniform density with radius 6.9 m and mass 270 kg is originally moving with velocity <2600, 0, 0> m/s, and is originally rotating with an angular speed 2 rad/s, in the direction shown in the diagram. A small piece of space junk of mass 9.8 kg is initially moving toward the satellite with velocity <−2200, 0, 0> m/s. The space junk hits the edge of the satellite as shown in the figure below, and moves off with a new velocity <−1300, 480, 0> m/s. Both before and after the collision, the rotation of the space junk is negligible. What is the rotational speed of the satellite after the collision?

This question can be answered through the conservation of angular momentum. The main equation needed is Iw(intial) (of the satellite) + hmv1sin(90-theta)(of the space junk) = Iw(final)(satellite) + hmv(final)sin(90-theta)(of the space junk) We are asked to solve for the final angular velocity, therefore w(final) = w(intial) + ((hm)/(2/5MR^2))*(v1-v2)cos(theta)

From here we plug and chug our known values,

the final answer is 9.822, we know the direction is positive (out of the page) because of the right hand rule.

Connectedness

Angular velocity is very useful when we need to figure out the angular momentum or even the rotational kinetic energy. Also it gives us another sense of how fast something is going, since linear velocity will not describe the velocity of something revolving. As most engineering majors are very physics intensive, it can be especially useful in practically any engineering application. Also it can also tell us certain aspects of a rotating object, or something going around a radius. Specifically to my major as an Industrial Engineer I can increase angular velocity and angular momentum to increase the efficiency in machinery which may be rotated and used to create products on an assembly line. A fairly interesting concept is that ballerinas and skaters use the conservation of angular momentum all of the time, in order to put on a show and spin faster they first out stretch their arms and one of their legs to increase their moment of inertia. Then to increase their spin or angular velocity they suddenly bring in their limbs therefore decreasing their moment of inertia, but due to the conservation of angular momentum their angular velocity increases to compensate for the decrease in the moment of inertia.

History

There is no person who officially "discovered" angular velocity. However ideas of angular momentum and inertia were initially formulated by Descartes, from there Issac Newton used it to help formulate his law of motions. When the two are put together law of conservation of momentum and also related Euler we also able to explicitly state that F=MA

Angular Velocity

Contents

Angular Momentum also known as Rotational velocity

A Mathematical Model

A Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu