Resistors and Conductivity

A resistor is a component of a circuit that acts to reduce both the flow of current and the voltage levels within the circuit. When current runs through a resistor, the energy stored within particles is converted to another form of energy, typically indicated by the emission of light or heat. Conductivity is a property of a given material that refers to the material's ability to transmit electricity. Conductivity and resistivity are opposites; that is, the higher the conductivity of a material, the less resistance it offers to the flow of current.

Relevant Equations

The resistance of a material can be calculated in several ways. The most common method relates resistance to the potential difference and the conventional current of the circuit, using the equation [math]\displaystyle{ R = {\frac{ΔV}{I}} }[/math] where ΔV is the potential difference across the resistor and I is the conventional current running through the circuit.

Another equation used to quantify resistance relates it to certain properties of the material and geometric properties of the resistor itself: [math]\displaystyle{ R = {\frac{L}{σA}} }[/math] where L is the length of the resistor, σ is the conductivity of the material, and A is the cross-sectional area of the resistor. This equation clearly demonstrates that resistivity and conductivity are inverses, as the conductivity constant can be found in the denominator.

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

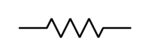
Symbol

The conventional symbol for a resistor used in electrical circuit diagrams is shown below.

Resistors in Series

When resistors are connected along a single path with no branches, they are said to be in series. Resistors in series are, in practice, equivalent to a single resistor with the combined resistance of its constituent resistors. In other words, [math]\displaystyle{ R_{equivalent} = R_1 + R_2 + R_3 + ... + R_n }[/math] for n resistors in series.

Because R = L/(σA), if every resistor is composed of the same material and has the same cross-sectional area, [math]\displaystyle{ L_{equivalent} = L_1 + L_2 + L_3 + ... + L_n }[/math]

Resistors in Parallel

When resistors are not connected in series, they can be connected in parallel, creating several branches within a circuit. Several resistors in parallel are, in practice, equivalent to a single resistor with a resistance that is the reciprocal of the sum of reciprocals of the individual resistances. In other words, [math]\displaystyle{ {\frac{1}{R_{equivalent}}} = {\frac{1}{R_1}} + {\frac{1}{R_2}} + {\frac{1}{R_3}} + ... + {\frac{1}{R_n}} }[/math] for n resistors in parallel.

Because 1/R = (σA)/L, if every resistor is composed of the same material and has the same length, [math]\displaystyle{ A_{equivalent} = A_1 + A_2 + A_3 + ... + A_n }[/math]

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page