Translational Angular Momentum

"Orbital" Angular Momentum Motion

Claimed by: Dhanusha Subramani

The Main Idea

Angular momentum describes the rotational motion of an object; it encompasses the translational and rotational angular momentum. The translational angular momentum deals with motion that can be described as orbital angular motion such as the orbits of the planets around the Sun in a bound system. When compared to the rotational angular momentum, we can see that the translational angular momentum doesn't take into account angular velocity or the inertia of the object(s); it simply deals with the distance(radius) and the momentum.

A Mathematical Model

The magnitude of Translational Angular Momentum is calculated using the magnitudes of the position and momentum vectors and the sin of the angle between the two vectors (θ). This is also technically equal to the cross product of the position and momentum vectors. (The position and momentum of the object are taken at a particular instant, so it is difficult to determine the object's future or past motion or path.)

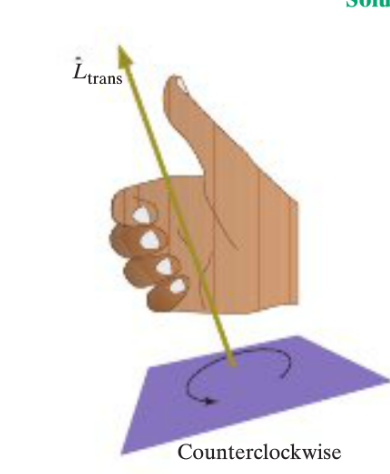
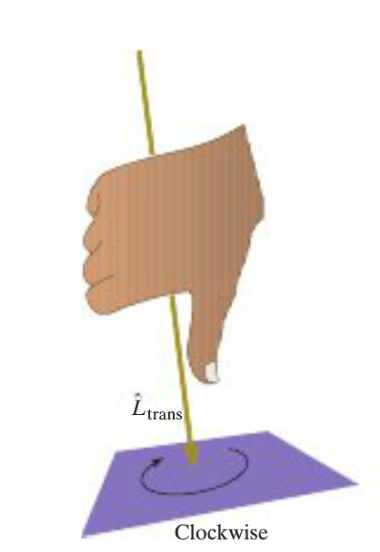
The direction of the Translational Angular Momentum can be determined using the right-hand rule. The positive z axis (+z) indicates that the object is moving counterclockwise in an xy plane while the negative z axis (-z) indicates that the object is moving counterclockwise.

In order to use the right hand rule, do the following: 1. Curl your fingers in the direction of the object's rotational motion (clockwise or counterclockwise). 2. Stick your thumb out while keeping your hand in the same position. The direction that your thumb is now pointing in is the direction of the angular momentum.

The thumb points out of the plane indicating that the direction is in the +z axis.

The thumb points into the plane indicating that the direction is in the -z axis.

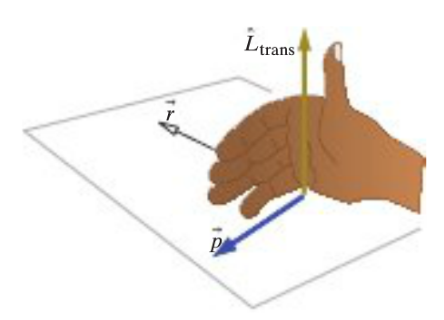
The direction can also be determined using the position and momentum vectors. In order to do this via the right hand rules, point your hand in the direction of the r vector (fingers should be pointing in its direction/path). Next, curl or fold your hand to point through the angle theta, so the palm of your hand should be facing the momentum vector. Stick your thumb out, and this unit vector represents the direction of the angular momentum vector.

The perpendicular component of the r vector represents the product of the position times the sine of the angle. This distance can be determined by drawing a line perpendicular to the momentum vector. The perpendicular distance is then the line that goes from the tail of the r vector to the line that the momentum vector points to.

File:PerpendicularTranslational.png

It is useful to think of the translational angular momentum as relative to a certain location, A, because this will help determine the momentum as specific to the location and instant, making the calculations more accurate and useful for application.

File:RelativeTranslational.png

A Computational Model

Teach hands-on with GlowScript

Here is some VPython coding that allows us to visual angular momentum in its two components (translational and rotational). When we run the code in VIDLE, we can see that there are two separate rods: the barbell which consists of the rod and two small masses and another rod which connects to the barbell. Both have rotational angular momentum, however, only the barbell exhibits translational angular momentum because of the change in its displacement as it rotates.

Examples

Simple

What is the angular momentum La if rA = vector 9,-9,0m and p = vector 12,10,0 kgm/s?

Here is also a very simple, straightforward example from the book.

Middling

Using the figure below, calculate the z component of the the translational angular momentum for each of the particle as defined by the plane below.

Here is also a similar example from Exam 4 following the same methodology and approach:

Connectedness

Connected to something I'm interested in: Connected to major: Interesting industrial application:

History

We can contribute the idea of orbits to Kepler. The idea of angular momentum itself, however, is credited to none other than Einstein.

See also

This topic relates to the entirety of angular momentum as a whole since it's the basis on which to build upon.

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page