Torque vs Work
PLEASE DO NOT EDIT THIS PAGE.
- UNDER CONSTRUCTION***********
- UNDER CONSTRUCTION***********
JeremyMD

When it comes to our universe, there still remains much that we do not understand. That we we do know and understand, we measure in relation to other ideas or subjects, in terms of abstracts we call units. In modern physics, and most mathematical applications we relate and measure matter and interactions in terms of these units. However, two such descriptions having the same units does necessarily connotate a representation of the same idea or measurement. Here, we will examine one such occurrence in modern physics, specifically the difference between torque and work when both are expressed as Newton*meters.
The Newton-Meter --> Vector vs Scaler
In modern physics, there a two concepts that, while describing different ideas, happen to utilize the same units, these units being:
[math]\displaystyle{ Newton * meters }[/math] [math]\displaystyle{ (N * m) }[/math]
Mathematical Model: The Concepts
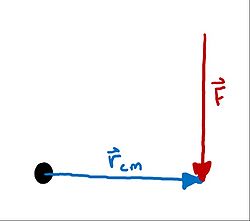
The first of these concepts is torque, which is a measurement of the moment that a force causes in a system. A moment is also known as a system's tendency of a force to cause rotation.
[math]\displaystyle{ \vec{\tau} = \vec{F} X \vec{r}_{cm} }[/math]
where [math]\displaystyle{ \tau }[/math] is the vector cross product of the force vector and position vector relative to the center of mass
The second concept is work, which is the measurement of a force acting over a distance on a given system.
[math]\displaystyle{ W = \vec{F}*\vec{r} }[/math]
where W is the scaler dot product of the force vector and change in position vector
Both of these concepts are measured using the units of [math]\displaystyle{ Newton * meters }[/math] , however torque is a vector value while work is a scaler value. This is a key point to keep in mind.
Previously, in Physics, when we addressed the energy principle and energy in general, we describe the measurement of energy and change in energy using the units:
[math]\displaystyle{ Joules }[/math] [math]\displaystyle{ (J) }[/math]
As it happens, work on a system is also equivalent to the change in kinetic energy of a system and therefore can also be expressed in joules. Positive work will add kinetic energy to a system whereas negative work will subtract kinetic energy from a system.
[math]\displaystyle{ W = ∆K = K_{final} - K_{initial} }[/math]
where W is the work done and K is the kinetic energy of the system.
So, work can be expressed in terms of joules, which means that torque can be expressed in terms of joules too, right? Well, it's not quite as straightforward as changing units. Remember, work is a scaler measurement, while torque is a vector representation. They must be measure individually because while work effects the linear momentum of a system, torque effects the angular momentum of a system. To put it in common terms, work relates to the movement of a system from one position to another while torque relates to the twisting of the system itself. So in fact, they represent very different concepts.
Nuances in Work
According to it's definition, work is a force acting over a given distance. So what about forces acting on an object that does not move? Let's look at an example. Take this block sitting on the earth and being acted on by a man who tries to lift it.
Let the mass of the block be [math]\displaystyle{ 5 kg }[/math] and the force of the man pulling up be [math]\displaystyle{ 20 N }[/math].
We know: [math]\displaystyle{ F = mg }[/math] where F is the force of gravity, m is the mass of the object, and g is the acceleration due to gravity
Force due to man: [math]\displaystyle{ F_{man} = 20 N }[/math]
Force due to gravity: [math]\displaystyle{ F_{grav} = (5 kg) * (-9.8 m/(s^{2}) = -49 N }[/math]
Net force: [math]\displaystyle{ F_{net} = 20 N + (-49 N) = -29 N }[/math]
However, we know that the block will not move through the earth due to the force of the earth acting on it, and so the block will stay in place. Since the block does not move there is no change in position. Applying this to our formula for work:
Work by man: [math]\displaystyle{ W_{man} = \vec{F}_{man} * \vec{r}_{block} = \lt 0, 20, 0\gt N * \lt 0, 0, 0\gt m = (0*0)Nm + (20*0)Nm + (0*0)Nm = 0 Nm }[/math]
So even though the man applied a force to the block, no work was done because the block did not move.
Nuances in Torque
Like work, torque also has some interesting situations that are important to take note of.
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
Middling
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
References
This section contains the the references you used while writing this page

