Iterative Prediction

Claimed by tconnors3

An Overview

The Momentum Principle is one of the fundamental principles in the study of mechanics and dynamics. By applying it to real world problems, the motion of systems can be modeled at specific points in time. Additionally, analyzing the implications of the momentum principle, physicists can not only pinpoint behavior of systems, but can also predict the motion of systems at specified times in the future.

A Mathematical Model

By starting from the general equation for the Momentum Principle, a formula can derived to predict the momentum of a given system at a specified point in the future. This is often referred to as the momentum update form of the Momentum Principle:

[math]\displaystyle{ {{(1)}\frac{d\vec{p}}{dt}}_{system} = \vec{F}_{net} }[/math]

[math]\displaystyle{ {{(2)}\vec{p}_{f} - \vec{p}_{i} = \vec{F}_{net}{Δt}} }[/math]

[math]\displaystyle{ {{(3)}\vec{p}_{f} = \vec{p}_{i} + \vec{F}_{net}{Δt}} }[/math]

Equation [math]\displaystyle{ {(3)} }[/math] gives the momentum update form of the momentum principle. As it shows, the momentum of a system can be predicted if the time period of the interaction and the external net force on the system are known. Momentum can be iteratively predicted like such for uniform or non-uniform time periods. Additionally, with update of momentum, velocity and position can be updated similarly to better reflect the motion over time of the system:

Velocity Update Formula:

[math]\displaystyle{ {\vec{v}_{f} = \vec{v}_{i} + \frac{{F}_{net}}{m}}{Δt} }[/math]

Position Update Formula:

[math]\displaystyle{ {\vec{r}_{f} = \vec{r}_{i} + \vec{v}_{avg}{Δt}} }[/math]

A Visual Model

As the momentum update formula suggests, the final momentum of a system after a given change in time should be the vector sum of the initial momentum (denoted [math]\displaystyle{ \vec{p}_{now} }[/math]) and the net force on the system multiplied by the scalar time change.

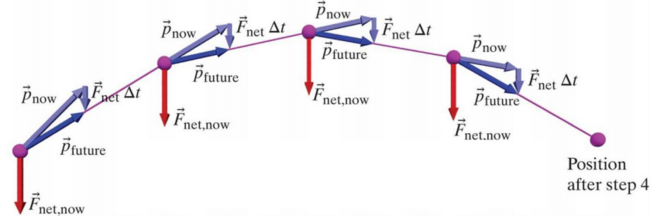
As the diagram suggests, each individual step can be analyzed through application of the momentum update form of the Momentum Principle. Once the final momentum is calculated, by utilizing the position and velocity update formulae, the final velocity and position of the system can be determined at the end of the time interval of interest.

Example Calculations

There are a variety of different problems that can be solved by utilizing the momentum update form of the Momentum Principle. They can vary in difficulty and require any number of iterations. It is often prudent to calculate these iterations in a program loop to save time and avoid miscalculations.

Example #1 - Momentum Update

A boy standing on level ground throws a 2 kg ball into the air at an initial velocity of [math]\displaystyle{ {\lt 8,6,0\gt m/s} }[/math]. If the only force acting on the ball is gravity, what is the final momentum of the ball after 0.2 seconds?

This problem can be solved simply by solving for final momentum in the momentum update equation:

[math]\displaystyle{ {\vec{p}_{f} = {m}\vec{v} + \vec{F}_{grav}{Δt}} }[/math]

[math]\displaystyle{ {\vec{p}_{f} = \lt 16,12,0\gt + \lt 0,-3.92,0\gt } }[/math]

[math]\displaystyle{ {\vec{p}_{f} = \lt 16,8.08,0\gt } }[/math]

Example #2 - Trajectory Maxima

A 1 kg ball is kicked from location [math]\displaystyle{ {\lt 9,0,0\gt m} }[/math] giving it an initial velocity of [math]\displaystyle{ {\lt -10,13,0\gt m/s} }[/math]. What is the maximum height that the ball will reach along its trajectory?

This problem is a bit more complicated than the previous one. Before calculating the maximum height of the ball, we must know the time it takes for the ball to reach its maximum height by analyzing the motion of the ball in the +y direction through the momentum update equation:

[math]\displaystyle{ {t}_{f} = {v}_{i,y}{m}/{F}_{net,y} }[/math]

[math]\displaystyle{ {t}_{f} = \frac{(13)(1)}{(1)(9.8)} = 1.326 s }[/math]

Now that we know how long it takes for the ball to reach its maximum height, we can solve for the final height of the ball by utilizing the position update equation:

[math]\displaystyle{ {r}_{f,y} = {r}_{i,y} + {v}_{avg,y}{Δt} }[/math]

[math]\displaystyle{ {r}_{f,y} = 0 + \frac{13+0}{2}(1.326) = 8.64 m }[/math]

Connectedness

How is this topic connected to something that you are interested in?
How is it connected to your major?
Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

References

Georgia Institute of Technology. Physics Department. PHYS 2211. Fall 2015. Wednesday, Week 2 Lecture Slides. Fenton, Flavio H

Georgia Institute of Technology. Physics Department. PHYS 2211. Fall 2015. Monday, Week 3 Lecture Slides. Fenton, Flavio H