Charged Disk
We will cover how to find the electric field of a uniformly charged disk, and how this can also apply to capacitors. (Shubham Shah)
The Main Idea
In this section, we will do a step-by-step process of calculating the electric field of a uniformly charged disk. This is especially important because two oppositely charged metal disks collectively are known as a capacitor, a concept seen in several places in physics and the real world.
A Mathematical Model
Before we begin our calculations, take a look at this image of a uniformly charged disk:
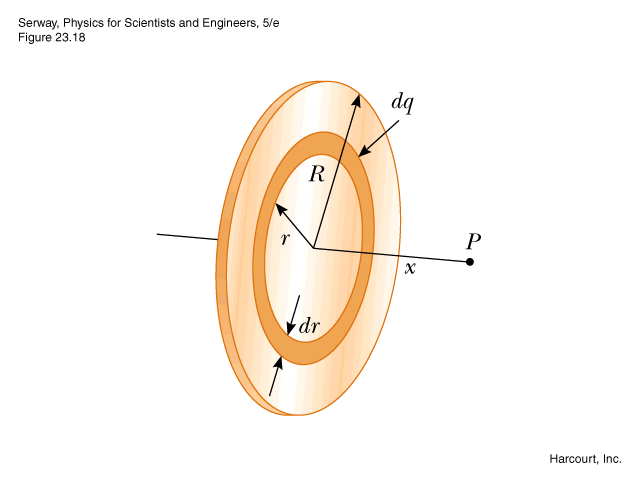
This image shows a visual representation of a disk. It should look pretty familiar. In fact, the shape of a disk is simply an extension of a ring. Think of it as infinitely many uniformly charged rings. Thinking of a disk this way will help to understand the equation of the electric field for a uniformly charged disk.
Recall the equation for the electric field of a uniformly charged ring:
[math]\displaystyle{ \ E= \frac{1}{4π\epsilon_0}\frac{qz}{(R^2+z^2)^{3/2}} }[/math]
This equation will tell you the electric field of a uniformly charged ring at any observation location z. To apply this equation to a disk, integration will be involved. The integration variable in this case should be the radius of the ring [math]\displaystyle{ r }[/math], as that will change with the infinitely many concentric rings you have. However, [math]\displaystyle{ r }[/math] is nowhere to be found in the equation. But if the radius of each ring is different, what gets affected as a result?
[math]\displaystyle{ \ dq= Q\frac{2πrdr}{πr^2} }[/math]
Here you see that the charge of each ring is different due to the changing radius. The charge changes by a factor of the area of the ring, [math]\displaystyle{ 2πrdr }[/math], (if you roll out the ring, it is a rectangle with height [math]\displaystyle{ dr }[/math] and width [math]\displaystyle{ 2πr }[/math]) divided by the area of the disk, [math]\displaystyle{ πr^2 }[/math]. Plugging that in for the q variable in our integration, and then cancelling out some variables, will allow us to solve for the electric field of a disk:
[math]\displaystyle{ \ dE = \frac{1}{2\epsilon_0}\frac{Q}{πR^2}\frac{zrdr}{(R^2+z^2)^{3/2}} }[/math]
Now we take the integral of this equation, and the result is this:
[math]\displaystyle{ \ E = \frac{1}{2\epsilon_0}\frac{Q}{πR^2}[1 - \frac{z}{(R^2+z^2)^{1/2}}] }[/math]
Thus, we have the equation that finds us the exact electric potential of a uniformly charged disk. You can still make approximations to make the formula simpler, however. If your observation location z is very close to the disk but not touching it, and is also significantly smaller than the radius of the disk (i.e. [math]\displaystyle{ 0 \lt \lt z \lt \lt R }[/math]), the equation becomes this:
[math]\displaystyle{ \ E = \frac{Q}{2\epsilon_0A} }[/math]
This is the most commonly seen form of this equation, and becomes very important when applied to the case of capacitors.
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
The writers of the textbook Matter and Interactions 3rd Edition, have some great examples of VPython code that show, in computational form, the electric field of a uniformly charged disk. To see the code in action, take a look at this or copy the code into your VIDLE shell. Enjoy!
Also took a look at this java applet for a lab simulation of a capacitor
Examples
An Concept Question
In what circumstance would you not use the approximate formula for calculating the electric field and have to use another formula?
This question is important, as this situation can come up a lot when solving physics problem. Remember that in the special case [math]\displaystyle{ 0 \lt \lt z \lt \lt R }[/math], you are allowed to use the approximate formula. But if that second condition, [math]\displaystyle{ z \lt \lt R }[/math], is not true, then you must use the exact formula (listed above). Or, if [math]\displaystyle{ 0 \lt \lt z }[/math], you also must use the exact formula, as then the observation location is relatively far from the disk. So it is important to look at your [math]\displaystyle{ z }[/math] value when you decide which equation to use when finding the electric field of a uniformly charged disk.
An Example Problem
A thin plastic disk of radius 0.4 m is uniformly charged with charge [math]\displaystyle{ Q = -4 * 10^{-7} C }[/math]. What is the electric field of this disk at a location [math]\displaystyle{ \lt 0.04, 0.06, 0\gt }[/math]m?
This is a a pretty simple problem, as [math]\displaystyle{ 0 \lt \lt z \lt \lt R }[/math], so you can use the approximate formula:
[math]\displaystyle{ \ E = \frac{4 * 10^{-7}}{2\epsilon_0π*(0.4)^{2}} = 4.5 * 10^{4} N/C }[/math]
Connectedness
Uniformly charged disks are a fundamental component to capacitors (which is two disks placed parallel to each other), which are found everywhere in physics courses as well as the real world. They are key parts of LC circuits, RC circuits, batteries, signal processing, and can even produce light.
See also
Further reading
Matter and Interactions 3rd Edition
External Links and References
Category: Electric Field