Iterative Prediction
By tconnors3
An Overview
The Momentum Principle is one of the fundamental principles in the study of mechanics and dynamics. By applying it to real world problems, the motion of systems can be modeled at specific points in time. Additionally, analyzing the implications of the momentum principle, physicists can not only pinpoint behavior of systems, but can also predict the motion of systems at specified times in the future.
A Mathematical Model
By starting from the general equation for the Momentum Principle, a formula can derived to predict the momentum of a given system at a specified point in the future. This is often referred to as the momentum update form of the Momentum Principle:
Equation [math]\displaystyle{ {(3)} }[/math] gives the momentum update form of the momentum principle. As it shows, the momentum of a system can be predicted if the time period of the interaction and the external net force on the system are known. Momentum can be iteratively predicted like such for uniform or non-uniform time periods. Additionally, with update of momentum, velocity and position can be updated similarly to better reflect the motion over time of the system:
[math]\displaystyle{ {\vec{v}_{f} = \vec{v}_{i} + \frac{\vec{F}_{net}}{m}}{Δt} }[/math]
Position Update Formula:
[math]\displaystyle{ {\vec{r}_{f} = \vec{r}_{i} + \vec{v}_{avg}{Δt}} }[/math]A Visual Model
As the momentum update formula suggests, the final momentum (shown here as [math]\displaystyle{ \vec{p}_{future} }[/math]) of a system after a given change in time should be the vector sum of the initial momentum (denoted [math]\displaystyle{ \vec{p}_{now} }[/math]) and the net force on the system multiplied by the scalar time change ([math]\displaystyle{ \vec{F}_{net}{Δt} }[/math]).
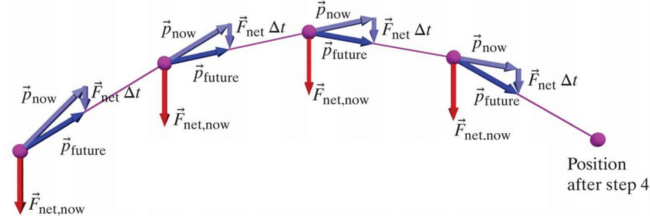
As the diagram suggests, each individual step can be analyzed through application of the momentum update form of the Momentum Principle. Once the final momentum is calculated, by utilizing the position and velocity update formulae, the final velocity and position of the system can be determined at the end of the time interval of interest.
Example Calculations
There are a variety of different problems that can be solved by utilizing the momentum update form of the Momentum Principle. They can vary in difficulty and require any number of iterations. It is often prudent to calculate these iterations in a program loop to save time and avoid miscalculations.
Example #1 - Momentum Update
A boy standing on level ground throws a 2 kg ball into the air at an initial velocity of [math]\displaystyle{ {\lt 8,6,0\gt m/s} }[/math]. If the only force acting on the ball is gravity, what is the final momentum of the ball after 0.2 seconds?
This problem can be solved simply by solving for final momentum in the momentum update equation:
Example #2 - Trajectory Maxima
A 1 kg ball is kicked from location [math]\displaystyle{ {\lt 9,0,0\gt m} }[/math] giving it an initial velocity of [math]\displaystyle{ {\lt -10,13,0\gt m/s} }[/math]. What is the maximum height that the ball will reach along its trajectory?
This problem is a bit more complicated than the previous one. Before calculating the maximum height of the ball, we must know the time it takes for the ball to reach its maximum height by analyzing the motion of the ball in the +y direction through the momentum update equation:
Now that we know how long it takes for the ball to reach its maximum height, we can solve for the final height of the ball by utilizing the position update equation:
Connectedness
Iterative Prediction serves as a basis for modeling complex motion throughout time. While some of the basic examples do not appear to be too trivial, iterative prediction can be used to solve more difficult problems. Having now almost completed a semester of mechanics, one topic that I became interested in almost right away was this idea of being able to solve problems in which we aren't necessarily concerned with the physics of the system at the current moment in time. Iterative Prediction of motion is just one of the many different techniques we have used to study the "physics of the future."
Iterative Prediction can have many applications to the field of Chemical Engineering, namely in the principles governing momentum transfer in chemical processes. A simple example is in studying fluid flow in a process. By making use of iterative prediction and the momentum principle, a chemical engineer can model the change in momentum of the fluid flow by analyzing the net force on the fluid (likely due to pressure) and the initial momentum of the fluid flow. In industry, this can be important so as to predict accumulation in a process and thus allow for modeling of an efficient process to maximize output.
History
The physics behind iterative prediction is nothing more than simple application of the momentum principle and projectile motion, which has existed in classical mechanics for quite some time. However, the practical application of iterative prediction for analyzing systems has evolved due to advances in computational methods and technology. With the computational power of a computer to iteratively calculate changes in momentum through time, one can analyze a system's motion extremely quickly without tedious and difficult mathematical calculations.
See also
There are many public resources that delve further into iterative prediction examples of more complex motion.
External links
MIT Open Courseware Introductory Mechanics
Iterative Prediction with VPython
References
Georgia Institute of Technology. Physics Department. PHYS 2211. Fall 2015. Wednesday, Week 2 Lecture Slides. Fenton, Flavio H
Georgia Institute of Technology. Physics Department. PHYS 2211. Fall 2015. Monday, Week 3 Lecture Slides. Fenton, Flavio H