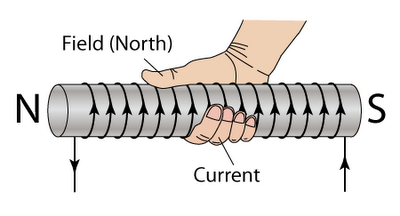
Magnetic Field of a Solenoid Using Ampere's Law

---- CREATED BY JAKE WEBB ----

This page explains how to use Ampere's Law to solve for the magnetic field of a solenoid.

The Main Idea

A solenoid is a long coil of wire with a very small diameter, often used to make electromagnets due to their ability to create strong magnetic fields. The magnetic field can be easily calculated along the axis of the solenoid using Ampere's Law, and the magnitude and direction of the field is constant throughout the entirety of the solenoid, excluding the ends.

As you can see in this model, at the ends of a solenoid the magnetic field begins to point outward at angles from the axis, with some of the field pointing directly perpendicular. In he middle, however, the field is constant throughout the entirety of the interior and is parallel to the axis.

A Mathematical Model

If there are [math]\displaystyle{ N }[/math] loops of wire the compose a solenoid of length [math]\displaystyle{ L }[/math], and we know that Ampere's Law for Magnetism gives us the form:

[math]\displaystyle{ {\oint\,\vec{B}•d\vec{l} = μ_{0}∑I_{inside path}} }[/math]

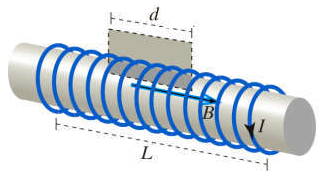
As stated above, the magnetic field inside a solenoid is constant and parallel to [math]\displaystyle{ dl⃗ }[/math], therefore Ampere's Law can be simplified to:

[math]\displaystyle{ BL=μ0NI }[/math]

By simply solving for [math]\displaystyle{ B }[/math] we can find the equation for the magnetic field of a solenoid:

[math]\displaystyle{ {B = \frac{μ_{0}NI}{L}} }[/math]

The direction can be found using the Right Hand Rule with your fingers curling around in the direction of the current and your thumb pointing in the direction of the magnetic field. It will always be along the axis for a solenoid.

A Computational Model

This gif shows how the magnetic field forms in the solenoid when there is a current running through it.

Examples

Simple

Find the magnetic field produced by the solenoid if the number of loops is 400 and current passing through on it is 5 A.( Length of the solenoid is 40cm)

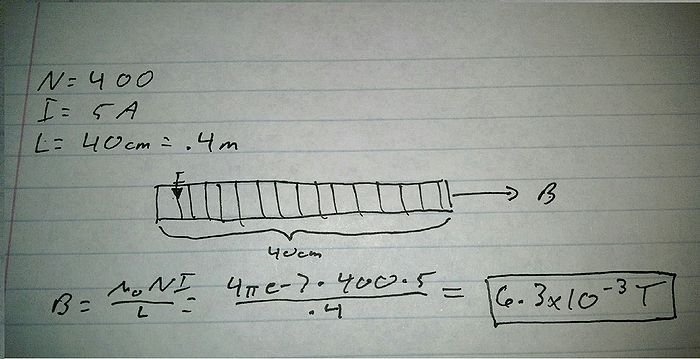
This example is very simple, as all of the variables of the equation are provided. All you need to do is plug them in and find the direction using the right hand rule.

Middling

A solenoid has a magnetic field of 5x10^-4 T, 3000 turns, and is 30 cm long. What is the current through the solenoid?

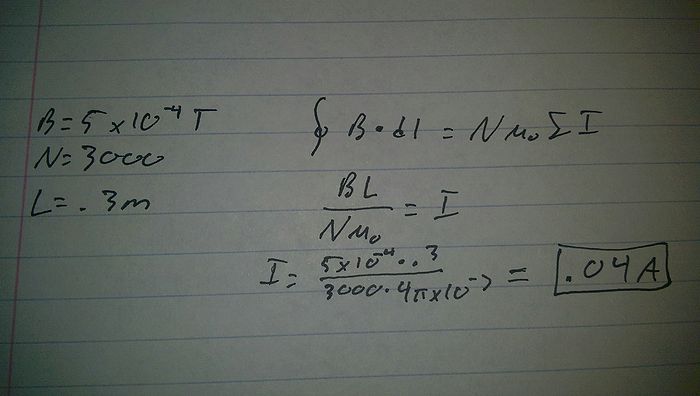
This example is just a reverse solving of the equation derived above for the magnetic field of a solenoid. It is not munch more difficult than the previous example.

Difficult

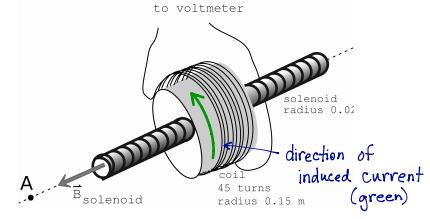
A long, tightly wound solenoid has a circular cross section of radius 0.02 m. The solenoid is connected to a power supply (not shown), and this current changes with time, so the magnetic field inside the solenoid also changes with time. At time t = 0 s, the magnitude of the magnetic field inside the solenoid is 1.8 T. At time t = 0.3 s, the magnitude of the magnetic field inside the solenoid is 0.5 T. The direction of the magnetic field inside the solenoid is shown in the diagram. The solenoid passes through a coil of wire, which has 45 turns of radius 0.15 m. The coil is connected to a voltmeter (not shown).

a.) At the same instant (t = 0.3 seconds), what will the absolute value of the reading on the voltmeter be?

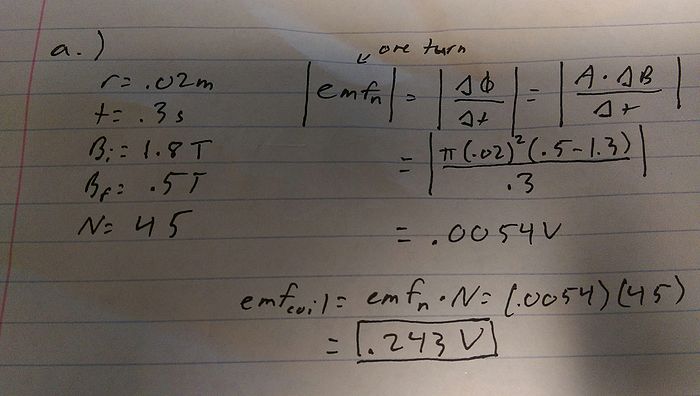
b.) The resistance of the coil is 2 ohms. At time t = 0.3 seconds, what is the conventional current in the coil?

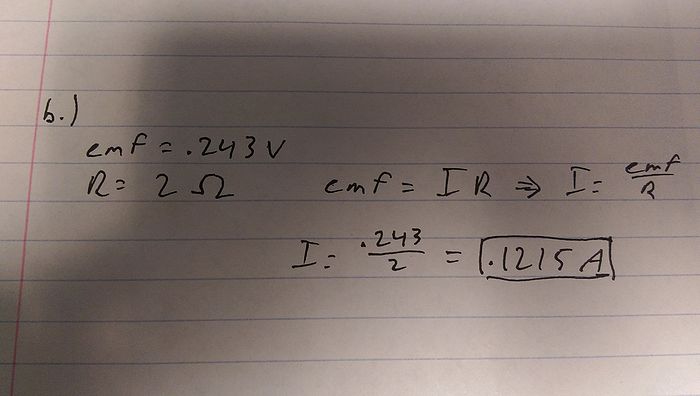
c.) At time t = 0.3 seconds, what is the magnitude of the non-coulomb electric field ENC in the coil?

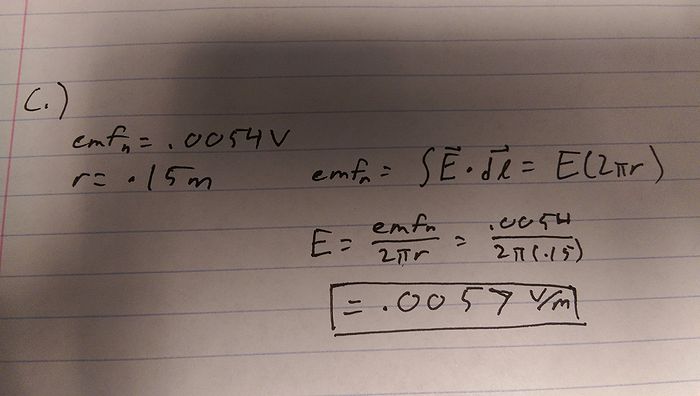
Connectedness

Solenoids are important because they are the easiest way to create electromagnets and are an important piece in transformers.
As a Computer Engineering major solenoids are important, at least for the EE parts of my major, because as stated above they are used to create transformers which are a major piece in large and small scale power grids.

Magnetic Field of a Solenoid Using Ampere's Law

Contents

The Main Idea

A Mathematical Model

A Computational Model

Examples

Simple

Middling

Difficult

Connectedness

See Also

Further Reading

External Links

References

Navigation menu