Vectors
'
Written by Elizabeth Robelo Improved by: Aparajita Satapathy
In physics, a vector is an object with a magnitude and a direction.
The Main Idea
A vector is an object with a magnitude and a direction. The magnitude of a vector is a scalar which represents the length of the vector. A vector is represented by an arrow. The orientation of the vector represents its direction. When a vector is drawn, the starting point is the tail and the ending point is called the head of the vector. Refer to the image below for a visual representation:
Visual Representation of a Vector
Vectors can be added and subtracted to each other. To add two vectors you put them head to tail. The connecting arrow starting from the tail of one to the head of the other is the new vector.
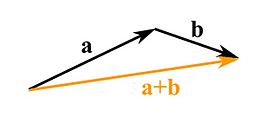
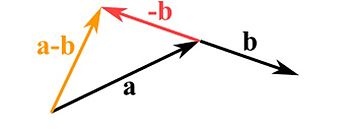
To subtract two vectors reverse the direction of the one you want to subtract and continue to add them like shown before.
A unit vector is a vector that points in the same direction as the original vector with magnitude 1. We usually designate the unit vector with a "hat" [math]\displaystyle{ {\hat{\imath}} }[/math]. The unit vector is often called the normal vector.
A Mathematical Model
Vectors are given by x, y, and z coordinates. They are written in the form <x, y, z> or xi + yj - zk. Magnitude: [math]\displaystyle{ |A| = \sqrt{x^2 + y^2 + z^2} }[/math]
Addition of two vectors: <a1, a2, a3> + <b1, b2, b3> = <a1 + b1, a2 + b2, a3 + b3>
Unit Vector: :[math]\displaystyle{ \mathbf{\hat{u}} = \frac{\mathbf{u}}{\|\mathbf{u}\|} }[/math]
A Computational Model
Here you have vpython code creating a vector from one object to another. vectors
Examples
Simple
Which of the following statements is correct?
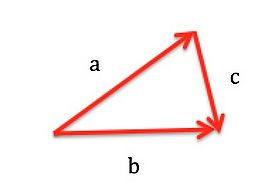
1. [math]\displaystyle{ \overrightarrow{c} = \overrightarrow{b} + \overrightarrow{a} }[/math]
2. [math]\displaystyle{ \overrightarrow{a} = \overrightarrow{b} - \overrightarrow{c} }[/math]
3. [math]\displaystyle{ \overrightarrow{a} = \overrightarrow{b} + \overrightarrow{c} }[/math]
4. [math]\displaystyle{ \overrightarrow{b} = \overrightarrow{a} + \overrightarrow{c} }[/math]
The answer is 2.
Middling
What is the magnitude of the vector C = A - B if A = <6, 21, 17> and B = <12, 7, 15>?
A - B = [math]\displaystyle{ \lt 6-12, 21-7, 17-15\gt = \lt -6, 14, 2\gt = C }[/math]
[math]\displaystyle{ \sqrt{(-6)^2 + 14^2 + 2^2} = 15.36 }[/math]
Difficult
What is the unit vector in the direction of the vector <12, -15, 9>? First you have to find the magnitude of the vector given: [math]\displaystyle{ \sqrt{12^2 + (-15)^2 + 9^2} = 21.21 }[/math]
Finally divide the vector by its magnitude to get the unit vector:
[math]\displaystyle{ \tfrac{\lt 12,-15,9\gt }{180} }[/math]
= <.565, -.707, .424>
Applications
You will use vectors for everything in physics ranging from velocity to gravitational field.
History
Giusto Bellavitis abstracted the basic idea of a vector in 1835 when he established the concept of equipollence. He called any pair of line segments of the same length and orientation equipollent. He found a relationship and created the first set of vectors.
The name vector was given to us by William Rowan Hamilton as part of his system of quaternions. The vectors he used were three dimensional.
Several other mathematicians developed similar vector systems to those of Bellavitis and Hamilton in the 19th century. The system used by Herman Grassman is the one that is most similar to the one used today. He thought of ideas similar to the cross product and vector differentiation.
See also
External links
References
https://www.mathsisfun.com/algebra/vectors.html
https://en.wikipedia.org/wiki/Euclidean_vector#Addition_and_subtraction